0
Les portes logiques (ou algèbre de Boole)... Ah là là...
C'est bien simple, sans elles, il n'y aurait ni électronique, ni informatique aujourd'hui
.
L'algèbre de boole est à la base de la logique de l'informatique moderne.
Il s'agit en fait de retranscrire de manière mathématique les signaux électriques.
Malgré ce nom barbare, les portes logiques sont extrêmement faciles à comprendre, il suffit juste d'un petit peu de logique.
Ici, nous allons juste expliquer les bases en étudiant les portes les plus connues.
Si l'interrupteur est ouvert, le signal électrique ne passe pas. On dira qu'il est à 0 (ou Faux).
On voit donc qu'ici, nous n'allons utiliser que deux chiffres : le 0 et le 1 puisque le courant ne peut avoir que deux états : il passe ou il ne passe pas. Nous travaillons donc dans un système binaire (à base 2).
Le processeur de votre ordinateur est composé de centaines de millions de transistors qui, assemblé d'une certaine façon permettent de créer des fonctions permettant de faire des calculs complexes.
Il s'agit en fait de règles qui sont basées sur quelques fonctions de base et qui sont finalement très logiques, mais simplement retranscrites de manière mathématique.
Admettons le circuit électrique suivant :
A et B sont des interrupteurs, Y est le signal à la sortie. Vous allez voir que nos tables de vérité vont se faire d'elles-même :
Nous définiront que si un interrupteur est fermé, cela veut dire qu'il laisse passer le courant. S'il est ouvert, il ne laisse pas passer le courant.
Maintenant réfléchissons :
Tout ça vous paraît logique ? (par pitié, c'est niveau 6° hein! )
Et bien sans le savoir, vous venez de définir votre première table de vérité.
En effet, rappelez-vous ce que nous avons dit plus haut. Considérons à 1 lorsque le courant passe et à 0 lorsqu'il ne passe pas. Nous pouvons, d'après notre réflexion synthétiser tout ceci dans un tableau :
Nous venons de définir la première table de vérité AND !
La fonction OU n'est pas plus difficile. Regardez le schéma suivant :
Et voilà notre deuxième table de vérité :
Il s'agit simplement de donner l'inverse du résultat initial. Si nous avons un 1 le NON 1 donnera 0, si nous avons 0, le NON 0 donnera 1.
Voici donc la table de vérité qui en découle :
Il s'agit simplement de la table de vérité du ET à laquelle le signal de sortie a subi une fonction NON. Cela donne :
Comme pour la fonction NAND, il s'agit de la table du OU sur laquelle nous appliquons la fonction NON à la sortie :
Il s'agit d'un cas particulier : la sortie sera vraie si et seulement si l'une des entrées est vraie mais pas les deux. La table de vérité qui en découle est très simple:
Voilà, c'est tout pour ce petit tuto "théorique" sur les portes logiques. J'espère que vous avez bien tout compris, sinon, direction le forum.
C'est bien simple, sans elles, il n'y aurait ni électronique, ni informatique aujourd'hui
.L'algèbre de boole est à la base de la logique de l'informatique moderne.
Il s'agit en fait de retranscrire de manière mathématique les signaux électriques.
Malgré ce nom barbare, les portes logiques sont extrêmement faciles à comprendre, il suffit juste d'un petit peu de logique.
Ici, nous allons juste expliquer les bases en étudiant les portes les plus connues.
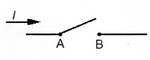
Si l'interrupteur est ouvert, le signal électrique ne passe pas. On dira qu'il est à 0 (ou Faux).
On voit donc qu'ici, nous n'allons utiliser que deux chiffres : le 0 et le 1 puisque le courant ne peut avoir que deux états : il passe ou il ne passe pas. Nous travaillons donc dans un système binaire (à base 2).
Le processeur de votre ordinateur est composé de centaines de millions de transistors qui, assemblé d'une certaine façon permettent de créer des fonctions permettant de faire des calculs complexes.
Il s'agit en fait de règles qui sont basées sur quelques fonctions de base et qui sont finalement très logiques, mais simplement retranscrites de manière mathématique.
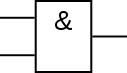
La fonction AND (ET)
Admettons le circuit électrique suivant :
A et B sont des interrupteurs, Y est le signal à la sortie. Vous allez voir que nos tables de vérité vont se faire d'elles-même :
Nous définiront que si un interrupteur est fermé, cela veut dire qu'il laisse passer le courant. S'il est ouvert, il ne laisse pas passer le courant.Maintenant réfléchissons :
- Si A est ouvert et B est ouvert, il n'y aura pas de courant à la sortie
- Si A est ouvert et B est fermé, il n'y aura pas de courant à la sortie
- Si A est fermé et B est ouvert, il n'y aura pas de courant à la sortie
- Si A est fermé et B est fermé, il y aura du courant à la sortie.
Tout ça vous paraît logique ? (par pitié, c'est niveau 6° hein! )Et bien sans le savoir, vous venez de définir votre première table de vérité.
En effet, rappelez-vous ce que nous avons dit plus haut. Considérons à 1 lorsque le courant passe et à 0 lorsqu'il ne passe pas. Nous pouvons, d'après notre réflexion synthétiser tout ceci dans un tableau :
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Nous venons de définir la première table de vérité AND !
La fonction OR (OU)
La fonction OU n'est pas plus difficile. Regardez le schéma suivant :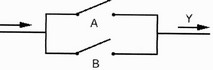
- Si A est ouvert ou B est ouvert, il n'y aura pas de courant à la sortie.
- Si A est ouvert ou B est fermé, il y aura du courant à la sortie.
- Si A est fermé ou B est ouvert, il y aura du courant à la sortie.
- Si A est fermé ou B est fermé, il y aura du courant à la sortie.
Et voilà notre deuxième table de vérité :| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
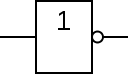
La fonction NOT (NON)
Il s'agit simplement de donner l'inverse du résultat initial. Si nous avons un 1 le NON 1 donnera 0, si nous avons 0, le NON 0 donnera 1.Voici donc la table de vérité qui en découle :
| A | Y |
| 0 | 1 |
| 1 | 0 |
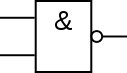
La fonction NAND (ou NOT-AND ou encore NON-ET)
Il s'agit simplement de la table de vérité du ET à laquelle le signal de sortie a subi une fonction NON. Cela donne :| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La fonction NOR (ou NOT-OR ou encore NON-OU)
Comme pour la fonction NAND, il s'agit de la table du OU sur laquelle nous appliquons la fonction NON à la sortie :| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
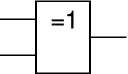
La fonction XOR (OU EXCLUSIF)
Il s'agit d'un cas particulier : la sortie sera vraie si et seulement si l'une des entrées est vraie mais pas les deux. La table de vérité qui en découle est très simple:| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Voilà, c'est tout pour ce petit tuto "théorique" sur les portes logiques. J'espère que vous avez bien tout compris, sinon, direction le forum.
