Préambule
Imaginons un moteur électrique qui commande un bras mécanique que l'on alimente avec une tension continue lui permettant d'atteindre 100 km/h. Ce moteur n'est pas capable de monter de 0 à 100 km/h instantanément à partir du moment où on l'alimente. Ce qui en soit semble embêtant pour que les gestes du bras mécanique soient précis. On va donc réguler ce moteur pour faire en sorte que ce soit le plus instantané possible à l'aide d'un système électrique qui entoure ce moteur. Et encore mieux, on va même faire en sorte qu'il soit rapide précis peut importe la consigne qu'on lui donne ! Il faut que ce moteur soit capable de reproduire et prendre en compte la consigne le plus exactement possible quoi qu'il arrive (usure, perturbations ...).
 Asservir et réguler, pour quoi faire ?
Asservir et réguler, pour quoi faire ?
- Améliorer les performances des systèmes.
- Asservir un système, c'est assurer sa stabilité.
- Réguler un système, c'est l'insensibiliser aux perturbations.
Un petit peu plus concrètement, l'asservissement d'un système permet de commander le moteur, par exemple, je vais envoyer à mon système une consigne qui va dire à mon moteur « tourne à 100 tour/minute s'il te plaît », le système va s'efforcer alors de prendre en compte cette consigne et de l'exécuter le plus efficacement possible. Nous verrons un plus tard ce que signifie,ici, « l'efficacité d'un système ».
On peut déjà distinguer plusieurs types d'asservissements, l'asservissement de vitesse décrit ci-dessus, l'asservissement de position et l'asservissement d'accélération que nous étudierons rapidement car il suffit de s'inspirer de l'asservissement de vitesse.
L'asservissement de position permet tout simplement d'envoyer une consigne qui va dire au moteur « fait ¼ de tour et arrête toi s'il te plaît », le moteur va donc encore une fois exécuter cette consigne plus ou moins bien selon l'asservissement qui sera mis en place. Et vous pourrez toujours essayer d'aller contre sa volonté, il sera toujours plus têtu que vous !
 Et l'électronique dans tout ça ?
Et l'électronique dans tout ça ?
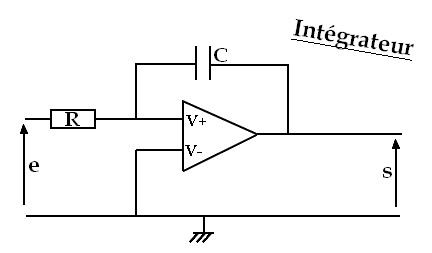
Ne vous en faites pas ! Un correcteur est composé de résistances, de condensateurs, de bobines, d'amplificateur opérationnel. Voici un exemple de correcteur, celui-ci est un intégrateur !
 Quels outils vont nous être utiles ?
Quels outils vont nous être utiles ?
D'un point de vue électronique, vous aurez besoin de connaître les lois générales de l'électricité, les composants comme les amplificateurs opérationnels. D'un point de vus mathématiques, ça se corse un peu, on va utiliser la transformée de Laplace (mais vous verrez c'est surmontable, je vous expliquerais), on va utiliser aussi énormément les diagrammes de bode, et un peu de black. Là encore vous ne serez pas lâcher dans la nature ! Les premières parties de ce tutoriel ne consisterons qu'à mettre en place tout les outils dont on a besoin pour étudier les asservissements. Cependant, il est nécessaire d'être à l'aise avec les équations, les simplifications, les fonctions.
 Je ne veux pas vous décourager mais je préfère tout de même vous prévenir, ce tutoriel est dur à comprendre, le niveau de difficulté est élevé. Je ferais donc en sorte de vous guider et vous aider un maximum.
Je ne veux pas vous décourager mais je préfère tout de même vous prévenir, ce tutoriel est dur à comprendre, le niveau de difficulté est élevé. Je ferais donc en sorte de vous guider et vous aider un maximum.
Prise en main des outils nécessaire à l'étude des asservissements
Laplace
Ça peut paraître un peu douloureux de débuter ce tutoriel avec la transformé de Laplace, mais c'est un mal nécessaire ! En effet, Laplace va nous simplifier la vie. La transformée de Laplace est en fait un outils mathématique qui va nous permettre de passer du domaine temporel ( le temps qui coule ...) au domaine fréquentiel (l'inverse du temps, f=1/T). Pour faire des asservissements, nous allons effectivement travailler dans le domaine fréquentiel et vous allez rapidement comprendre pourquoi.
 Attention! La transformé de Laplace ne nous fait pas vraiment en réalité passer du domaine du temps au domaine fréquentiel, mais pour un souci de simplicité, vous pouvez le considérer tout de même. (Laplace nous fait passer dans le domaine de Laplace)
Attention! La transformé de Laplace ne nous fait pas vraiment en réalité passer du domaine du temps au domaine fréquentiel, mais pour un souci de simplicité, vous pouvez le considérer tout de même. (Laplace nous fait passer dans le domaine de Laplace)
Je vais enfin pouvoir vous apporter la preuve que Laplace c'est merveilleux ! Je ne devrais pas vous apprendre le contenu de ce tableau (même si je vous l'apprends et qu'il vous fait peur restez là tout de même, Laplace est là pour vous sauver :
Composant : Tension à ses bornes dans le domaine du temps
résistance : 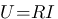
condensateur : 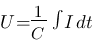
bobine : 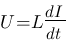
Voyez-vous tout ces termes d'intégrale et de dérivée un peu barbare. Regardons donc maintenant ce que ça donne avec Laplace ( la variable n'est plus t comme dans le domaine temporel mais p pour domaine de Laplace).
Composant : Tension à ses bornes dans le domaine de Laplace
résistance : 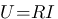
(il n'y avait même pas de variable t donc il n'y a pas de raison que ça change)
condensateur : 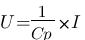
bobine : 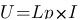
Et là miracle !!! Les intégrales et les dérivées disparaissent au profit de stupides multiplications et divisions. Lorsque l'on est dans le domaine de Laplace, on parle d'impédance d'une résistance ® d'un condensateur (1/Cp) ou d'une bobine (Lp). Ainsi on peut appliqué à ces 3 composants la loi d'ohm: U = impédance * I. Vous étiez loin de vous imaginer qu'asservir c'était simplement utilisez la loi d'ohm non ?
 Attention ! Ce qui suit vous n'êtes pas obligé de lire pour comprendre la suite de ce tutoriel, ce sont juste des formules de la transformée de Laplace, il ne faut pas oublier qu'elles existent ...
Attention ! Ce qui suit vous n'êtes pas obligé de lire pour comprendre la suite de ce tutoriel, ce sont juste des formules de la transformée de Laplace, il ne faut pas oublier qu'elles existent ...
Allez finis de s'amuser, si on veut réellement lier le domaine temporel au domaine de Laplace il va falloir passer par ces formules qui donnent légèrement le tournis :
Définition :
La transformée de Laplace d'une fonction f(t) vaut l'intégrale de l'exponentiel de -pt multiplier par f(t). On le note :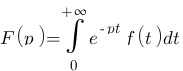 ou F(p) est la transformée de Laplace de f(t).
ou F(p) est la transformée de Laplace de f(t).
Vous êtes encore là ?? Ne vous enfuyez pas en courant ! On ne va pas l'utiliser ! Si toute fois vous tenez à avoir un exercice pour utiliser cette définition, faites moi signe !!
Propriétés :
Linéarité : 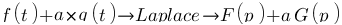 avec F(p) la transformée de Laplace de f(t) et G(p) la transformée de Laplace de g(t).
avec F(p) la transformée de Laplace de f(t) et G(p) la transformée de Laplace de g(t).
Facteur d'échelle : 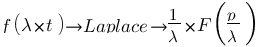
Théorème du retard : 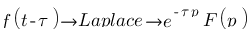
Dérivation : 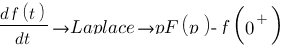
Intégration : 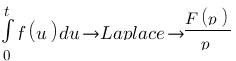
Théorèmes :
de la valeur initiale : 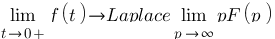
de la valeur finale : 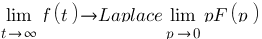
 Attention ! Ceux qui ont survolé toutes ces formules, il va falloir être de nouveau un petit peu plus attentif pour ce qui suit !
Attention ! Ceux qui ont survolé toutes ces formules, il va falloir être de nouveau un petit peu plus attentif pour ce qui suit !
Vous vous rendez bien compte que transformer une fonction qui dépend du temps en une fonction qui dépend de p, ce n'est pas évident et assez laborieux, c'est pourquoi il existe un tableau avec des résultats (presque) tout prêts ! Voici ce tableau :
| Domaine fréquentiel (Laplace) | Domaine temporel |
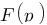 |
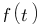 |
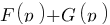 |
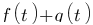 |
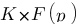 |
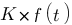 |
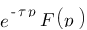 |
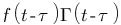 |
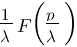 |
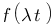 |
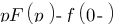 |
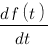 |
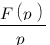 |
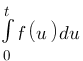 |
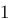 |
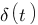 |
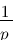 |
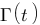 |
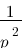 |
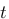 |
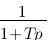 |
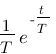 |
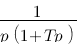 |
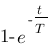 |
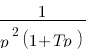 |
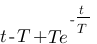 |
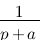 |
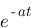 |
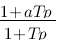 |
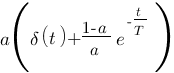 |
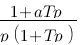 |
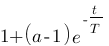 |
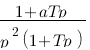 |
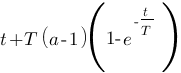 |
 |
 |
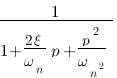 |
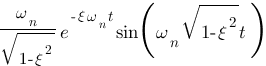 |
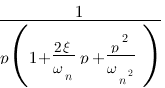 |
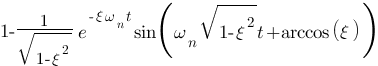 |
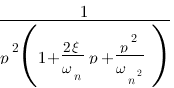 |
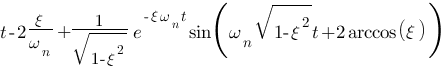 |
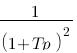 |
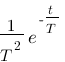 |
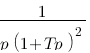 |
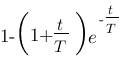 |
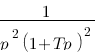 |
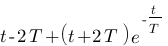 |
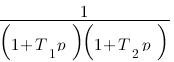 |
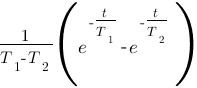 |
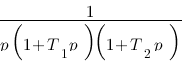 |
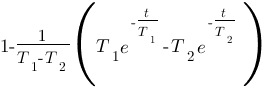 |
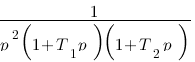 |
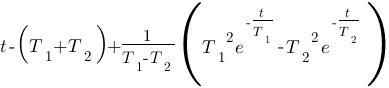 |
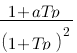 |
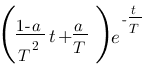 |
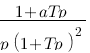 |
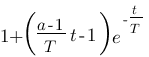 |
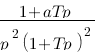 |
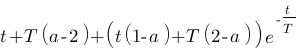 |
 On va s'en servir beaucoup de ce tableau ???
On va s'en servir beaucoup de ce tableau ???
Rassurez-vous, non on va éviter de s'en servir (bien que ce soit utile de savoir le faire pour asservir) parce que c'est un peu compliqué, cependant je vous propose un exercice dans le chapitre suivant pour les plus téméraires.
Bon et bien voilà ! Vous voilà enfin prêt à calculer les fonctions de transfert, vous verrez, ce sera plus simple que ce chapitre là. Je comprends que ce tutoriel puisse vous paraître difficile et que l'on puisse se demander à quoi tout ça ça peut servir !? Mais je vous assure que nous en avons besoin pour asservir nos moteurs ! Bon courage.
Les fonctions de transfert
Ce chapitre va permettre de mettre en équation n'importe quel système électrique !
Les systèmes que nous allons étudier (correcteurs, moteur et capteurs) possèdent une tension d'entrée, une tension de sortie et une masse commune. La fonction de transfert de ce système est alors la tension de sortie divisée par la tension d'entrée. Nous allons avoir besoin de connaître les fonctions de transfert des correcteurs de nos processus pour déterminer toutes ses caractéristiques. Nous allons bien évidement utiliser le domaine fréquentiel pour calculer les fonction de transfert parce que c'est ... beaucoup plus facile ! Sans plus attendre, voyons comment on fait à travers un exemple ! Nous allons choisir un circuit RC que voici :

Notre objectif est d'exprimer Vs et Ve en fonction de l'impédance des composants de ce système. Ce cas est simple, il suffit d'utiliser le diviseur de tension. Je préfère préciser qu'il est possible appliquer un diviseur de tension car nous travaillons avec les impédances et Laplace ! L'impédance de la résistance vaut R, et celle du condensateur vaut 1/Cp (comme nous avons vu dans le chapitre précédent). Appliquons le diviseur de tension :
On a donc : 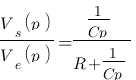 , cette relation est correcte, cependant il vaut mieux l'exprimer de la forme « polynôme de degré n / polynôme de degré n' ». On va multiplier par Cp en haut et en bas ce qui donne :
, cette relation est correcte, cependant il vaut mieux l'exprimer de la forme « polynôme de degré n / polynôme de degré n' ». On va multiplier par Cp en haut et en bas ce qui donne : 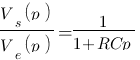 . Et voilà le travail ! Vous venez de calculer votre fonction de transfert de ce système ! Imaginez comme Laplace simplifie les calculs ! Si vous êtes courageux, vous pourriez exprimer cette fonction de transfert en fonction du temps en utilisant le tableau vu précédemment et vous trouveriez que :
. Et voilà le travail ! Vous venez de calculer votre fonction de transfert de ce système ! Imaginez comme Laplace simplifie les calculs ! Si vous êtes courageux, vous pourriez exprimer cette fonction de transfert en fonction du temps en utilisant le tableau vu précédemment et vous trouveriez que : 
Cet exemple est un peu trop simple non ? Allez, il faut s'entraîner ! Et si on reprenait le schéma de l'intégrateur de l'introduction !
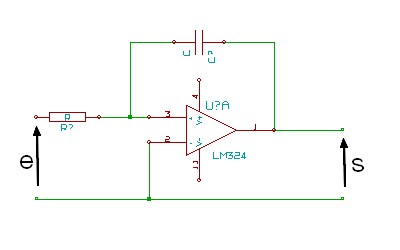
L'amplificateur est idéal donc V+ = V- . Avec les amplificateurs opérationnel, mieux vaut travailler avec les courants. Le courant qui passe dans R est le même que celui qui passe dans C car le courant est nulle aux bornes 3 et 2. La tension aux bornes de R vaut Ve – V+ et la tension aux bornes de C vaut V+ - Vs. On à donc : 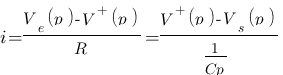 . V- est relié à la masse donc V- = 0, or V+ = V- donc V+ = 0. On a alors :
. V- est relié à la masse donc V- = 0, or V+ = V- donc V+ = 0. On a alors : 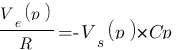 , il n'y a plus qu'a exprimer ce résultat sous forme conventionnel :
, il n'y a plus qu'a exprimer ce résultat sous forme conventionnel : 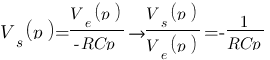 Et voilà c'est fini !
Et voilà c'est fini !
Juste pour votre culture générale, toute fonction de transfert qui possède le terme 1/p est un intégrateur. On va également dire que ce système est inverseur à cause du « - ». Ce correcteur est donc un intégrateur inverseur ! Nous verrons plus tard les détails de ce type de correcteur.
Imaginons maintenant que nous mettions ces deux montages bout à bout :
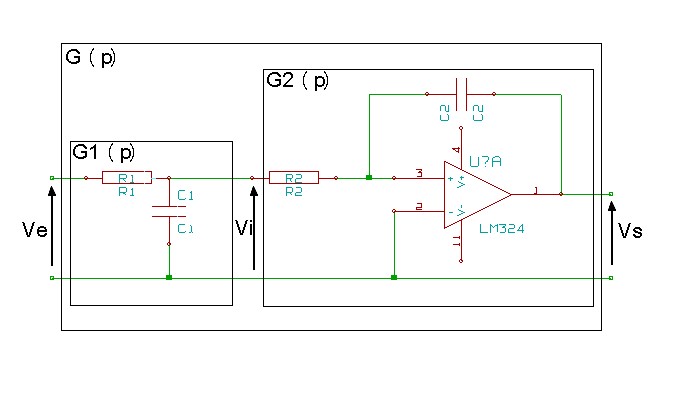
Calculons alors la fonction de transfert de l'ensemble ! Supposons que R1=R2=R et que C1=C2=C On à vu que 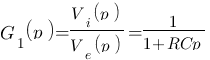 et que
et que 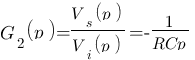 . Multiplions les donc entre eux pour obtenir la fonction de transfert de l'ensemble :
. Multiplions les donc entre eux pour obtenir la fonction de transfert de l'ensemble : 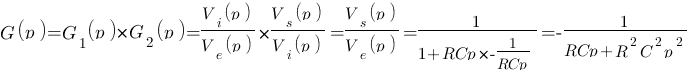
Nous avons multiplié deux systèmes d'ordre 1, G1(p) et G2(p) (le plus haut degré est 1 => 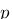 ) pour obtenir un système d'ordre 2 G(p) (le plus haut degré est 2 =>
) pour obtenir un système d'ordre 2 G(p) (le plus haut degré est 2 =>  ).
).
 Attention ! Ceci n'est pas toujours vrai ! Ce n'est pas parce que l'on place l'un derrière l'autre deux montage d'ordre 1 que le tout forme un montage d'ordre 2.
Attention ! Ceci n'est pas toujours vrai ! Ce n'est pas parce que l'on place l'un derrière l'autre deux montage d'ordre 1 que le tout forme un montage d'ordre 2.
Vous êtes maintenant paré pour trouver toutes les fonctions de transferts de tout nos futurs correcteurs ! Cependant, bien que nous ayons presque tout les outils nécessaires pour entrer dans le vif du sujet nous allons nous appesantir sur une dernière chose, les diagrammes de bode ! En effet, toute fonctions de transfert possède sont diagramme de bode, c'est LA (mais pas l'unique) représentation graphique d'une fonction de transfert, donc d'un système !
Les diagrammes de bode
Toutes fonctions de transfert peut s'exprimer graphiquement à l'aide d'un diagramme de bode. Pour construire ce diagramme de bode il y a deux techniques. Une technique générale qui marche à tout les coups mais qui est compliquée mathématiquement, une technique « légo » qui est beaucoup plus simple mais qui ne fonctionne pas forcément dans tout les cas. C'est cette dernière que nous utiliserons dans la suite du tutoriel, cependant je vais rapidement vous exposer la technique générale.
 Un diagramme de bode ça ressemble à quoi ??
Un diagramme de bode ça ressemble à quoi ??
Un diagramme de bode est constitué de deux graphiques munis chacun d'un repère x,y.
- Le premier graphique est la représentation du gain (amplitude) de la fonction de transfert exprimé en décibel (dB) en fonction de oméga 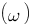 .
.
- Le second graphique est la représentation de la phase (argument) de la fonction de transfert exprimé en radian par seconde (rad/s) en fonction de oméga 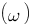 .
.
Expliquons un peu ces termes barbares, tout d'abord oméga est en fait quasiment la même chose qu'une fréquence puisque 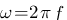 . Nous allons donc exprimer le gain et la phase de la fonction de transfert en fonction de la fréquence. Ensuite les décibel représente l'atténuation d'un signal électrique dans notre cas (en acoustique, les dB représente l'atténuation du bruit). Ainsi, plus la valeur en dB est faible et plus le signal électrique sera atténué (tout comme le dB acoustique, plus ils sont faible et moins ça fait de bruit !). La phase représente le décalage qu'auront entre eux le signal d'entrée (Ve) et le signal de sortie (Vs) du système électrique.
. Nous allons donc exprimer le gain et la phase de la fonction de transfert en fonction de la fréquence. Ensuite les décibel représente l'atténuation d'un signal électrique dans notre cas (en acoustique, les dB représente l'atténuation du bruit). Ainsi, plus la valeur en dB est faible et plus le signal électrique sera atténué (tout comme le dB acoustique, plus ils sont faible et moins ça fait de bruit !). La phase représente le décalage qu'auront entre eux le signal d'entrée (Ve) et le signal de sortie (Vs) du système électrique.
Une dernière petite chose avant de passer aux deux techniques de tracés, dans nos fonctions de transfert, pour tracer leur diagramme de bode, on va remplacer « p » par 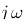 . Vous savez maintenant ce que représente oméga, et le « j » lui vient du fait que derrière la variable p, c'est un nombre complexe qui se cache (a+jb). Si vous ne connaissez pas les nombres complexes laissez tomber, vous vous en sortirez avec la seconde technique, admettez seulement qu'il faut remplacer « p » par
. Vous savez maintenant ce que représente oméga, et le « j » lui vient du fait que derrière la variable p, c'est un nombre complexe qui se cache (a+jb). Si vous ne connaissez pas les nombres complexes laissez tomber, vous vous en sortirez avec la seconde technique, admettez seulement qu'il faut remplacer « p » par 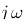 . La fonction de transfert G(p) devient alors
. La fonction de transfert G(p) devient alors 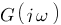 .
.
Voici un exemple de diagramme de bode (gain et phase) :
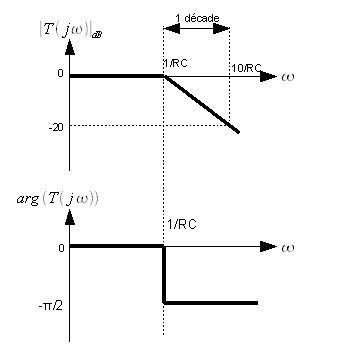
Première Technique
Si vous ne connaissez ni le logarithme décimal ni les nombres complexe (programme de terminal S), passez directement à la seconde technique.
Il suffit de calculer les quelques points en utilisant ces formules :
- Pour le gain : 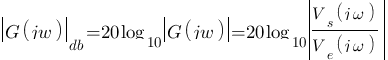
- Pour la phase : 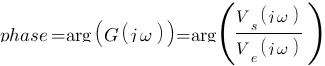
Sympathique non ? ![]() Bon courage ! Je vous proposerais un exercice si vous souhaitez vous entraîner.
Bon courage ! Je vous proposerais un exercice si vous souhaitez vous entraîner.
Seconde Technique
Cette technique requiert moins de connaissances en mathématique. On va jouer aux légos ! Le principe c'est d'assembler quelques diagrammes de référence pour obtenir celui que nous désirons. Nous avons donc besoin d'un peut de documentation toujours à côté de nous pour nous en sortir ( à moins de connaître les diagrammes de référence par cœur ...), les voici :
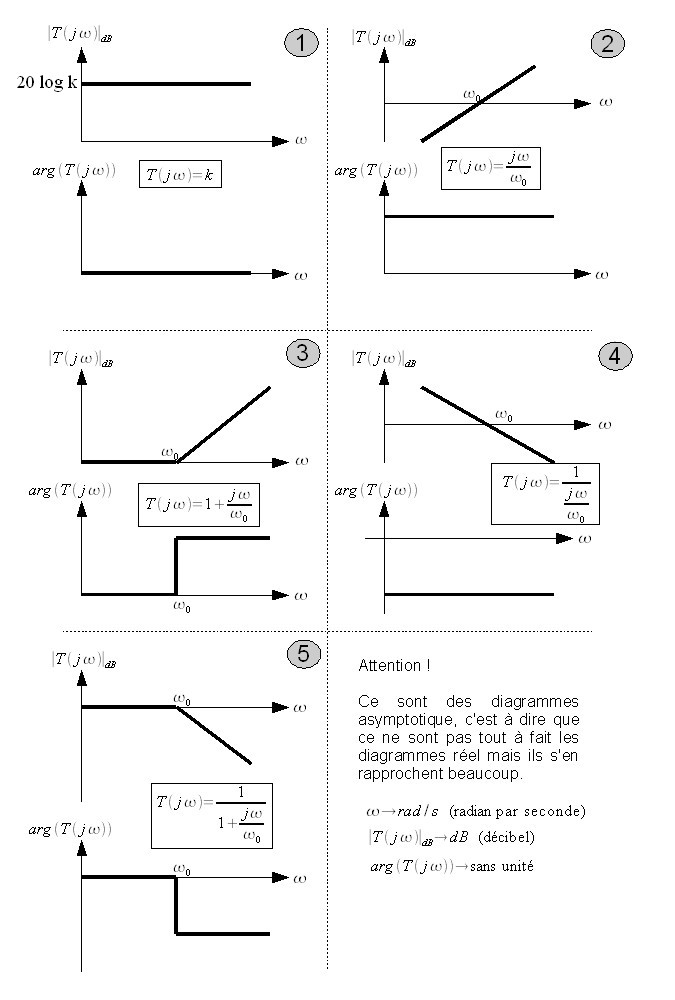
Informations Complémentaires :
A propos du 20 log k , si vous ne connaissez pas les logarithmes, pas de panique, munissez vous d'une calculatrice qui possède la touche/fonction « log ». Et tapez 20 * log k (en remplaçant k par sa valeur).
A propos du +/- 20 dB décade, sachez que l'on gradue un diagramme de bode en décades, c'est à dire, au lieu de graduer respectivement 1,2,3,4,5,6 on gradue 1,10,100,1 000,10 000, 100 000 (on peut aussi aller dans les chiffres à virgule 0,0001 , 0,001 , 0,01 , 0,1 , 1 , 10 ... ). Une décade représente l'écart entre 2 graduations, par exemple, de 10 à 100 on à une décade, ou bien de 0,1 à 1 on a aussi 1 décade, de 100 10 000 on à deux décades ! Quel est l'intérêt d'une telle graduation ? Compresser les fréquences trop faible ou trop haute et mettre en valeur les fréquences intermédiaires ( au niveau du 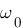 ). Ainsi lorsque c'est écrit +20dB/décade, c'est que l'on augmente de 20 dB lorsque l'on parcours une décade ( si à
). Ainsi lorsque c'est écrit +20dB/décade, c'est que l'on augmente de 20 dB lorsque l'on parcours une décade ( si à 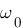 on est à 20dB alors à 10
on est à 20dB alors à 10 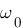 on sera à 40 dB, à 100
on sera à 40 dB, à 100 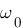 à 60 dB, à 1 000
à 60 dB, à 1 000 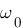 à 80 dB et ainsi de suite ) à l'inverse -20dB/décade signifie qu'on l'on diminue de 20 dB lorsque l'on parcours une décade.
à 80 dB et ainsi de suite ) à l'inverse -20dB/décade signifie qu'on l'on diminue de 20 dB lorsque l'on parcours une décade.
Illustration des échelles :
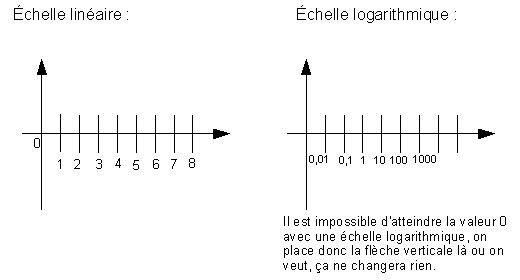
Au lieu de mettre 0,01 , 0,1 , 1 , 10 , 100 on aurai pu mettre 0,01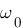 , 0,1
, 0,1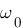 , 10
, 10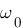 , 100
, 100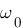 , ça ne change rien l'échelle reste toujours logarithmique car il y a un facteur 10 entre chaque termes.
, ça ne change rien l'échelle reste toujours logarithmique car il y a un facteur 10 entre chaque termes.
Exemples :
Reprenons alors nos fonctions de transfert du chapitre précédent pour trouver leur diagramme de bode. Nous avions tout d'abord obtenu celle-ci 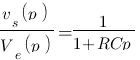 , remplaçons p par
, remplaçons p par 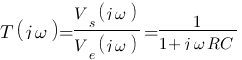 , on remarque qu'elle se rapproche beaucoup du modèle numéro 5 :
, on remarque qu'elle se rapproche beaucoup du modèle numéro 5 : 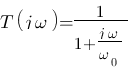 faisons l'analogie entre les deux
faisons l'analogie entre les deux 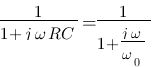 , on a alors
, on a alors 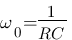 . Le diagramme de bode de cette fonction de transfert est donc :
. Le diagramme de bode de cette fonction de transfert est donc :

Ce cas reste simple, nous allons compliquer un tout petit peu pour illustrer un piège. Immaginez que nous ayons cette fois comme fonction de transfert 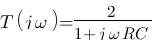 , elle est presque identique à celle d'avant mais il faut faire très attention au 2 au dessus de la fraction qui est différent du modèle ! Cette fonction de transfert est en fait maintenant le combiné de deux modèles, le modèle numéro 1 avec celui du numéro 5 !
, elle est presque identique à celle d'avant mais il faut faire très attention au 2 au dessus de la fraction qui est différent du modèle ! Cette fonction de transfert est en fait maintenant le combiné de deux modèles, le modèle numéro 1 avec celui du numéro 5 ! 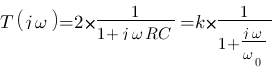 avec k = 2 et
avec k = 2 et 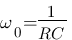 . Ce qui est pratique c'est que lorsque l'on multiplie les modèles entre eux, et bien on additionne les diagrammes correspondant entre eux ! (Ceci est du au fait que log(a*
. Ce qui est pratique c'est que lorsque l'on multiplie les modèles entre eux, et bien on additionne les diagrammes correspondant entre eux ! (Ceci est du au fait que log(a*![]() = log a + log b ). On va alors additionner les diagrammes suivant :
= log a + log b ). On va alors additionner les diagrammes suivant :
Celui de 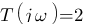
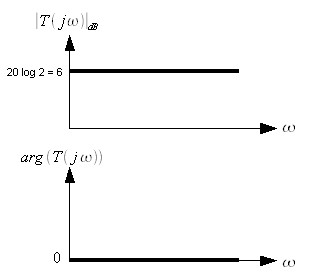
Avec celui trouver précédemment :

Ce qui nous fait :
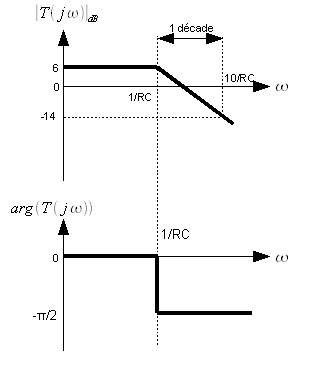
Et voilà le travail ! La courbe du gain est juste monté de 6 dB (20log2) et celle de la phase n'a pas bougé car la phase de T(jw) = k est toujours nulle. Avec l'habitude, on ne décrit plus cette manipulation, on remonte la courbe de 20 log k lorsqu'il y a un facteur k devant la fonction de transfert et ça suffit bien !
On va chercher le diagramme de bode d'un dernier système avant de passer à autre chose, on complique encore un peu ! Vous vous souvenez sûrement de ce système là :

Nous avions trouver les résultats suivant :
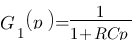
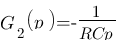
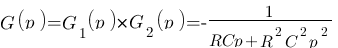
Remplaçons p par 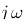 :
:
 Attention ! Considérez le résultat suivant :
Attention ! Considérez le résultat suivant : 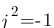 , de plus on peut se permettre d'enlever le « - » de G2, il ne modifiera pas les résultats si ce n'est que Vs ne sera pas inversé.
, de plus on peut se permettre d'enlever le « - » de G2, il ne modifiera pas les résultats si ce n'est que Vs ne sera pas inversé.
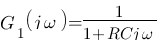
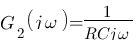
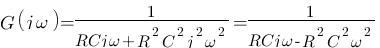
Malheureusement, G(p) ne correspond à aucun modèle ![]() . Rassurez vous, il suffit de se mettre en mode légo ! N'oubliez pas que
. Rassurez vous, il suffit de se mettre en mode légo ! N'oubliez pas que 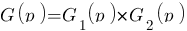 donc il suffit d'additionner les diagrammes de G1 et G2, et heureusement ils correspondent à un modèle ! Le G1, on l'a déjà fait au dessus donc ça ne change pas :
donc il suffit d'additionner les diagrammes de G1 et G2, et heureusement ils correspondent à un modèle ! Le G1, on l'a déjà fait au dessus donc ça ne change pas :

Le G2 correspond au modèle 4 ! Vous avez compris le système donc je ne repose pas tout les calculs, on trouve que 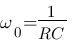 . On peut alors dessiner le diagramme :
. On peut alors dessiner le diagramme :
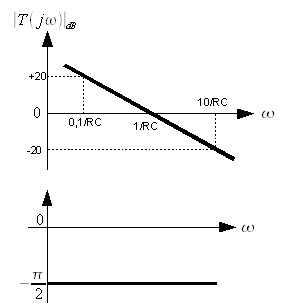
Additionnons les deux :
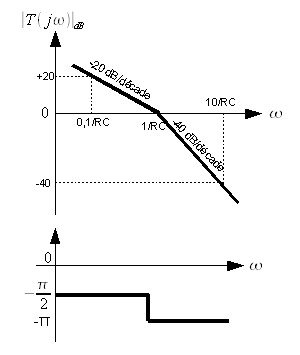
Et voilà le travail ! Cette fois tout a changé ! On pourrait encore réussir à compliquer le diagramme d'un tel système si l'on choisissait R1 différent de R2 et/ou C1 différent de C2, dans un tel cas on aurait des différents omega_0 pour G1 et G2.
On va pouvoir enfin rentrer dans le vif du sujet, nous possédons tout les outils qui vont nous permettre d'étudier l'action des correcteurs. Je tiens tout de même à vous féliciter si vous avez tout suivi et compris correctement tout ce qu'on a vu jusque là, rien n'est loin d'être évident, maintenant on va voir des choses plus pratique et agréable !
Les systèmes
Schémas
Tout système peut se représenter sous forme de schéma muni de blocs pour distinguer les différentes parties, ils sont nécessaire pour s'y retrouver !
Chaque bloc possède une ou des entrées ainsi qu'une ou des sorties. Voici comment on pourrait représenter un moteur :
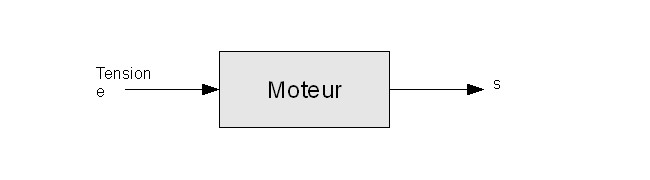
Évidemment, un moteur à besoin d'une tension d'entrée « e » pour tourner, et d'un capteur de vitesse pour contrôler celui-ci. Ce capteur renvoi une tension « s » image de la vitesse. Cependant, si on le laisse en l'état, le moteur va être laissé un peu à lui même. Rajoutons-lui un correcteur C(p) ! Le moteur, lui, possède sa propre fonction de transfert que l'on va nommer G(p) qui décrit comment il réagit . On va également poser un peu de vocabulaire utile.
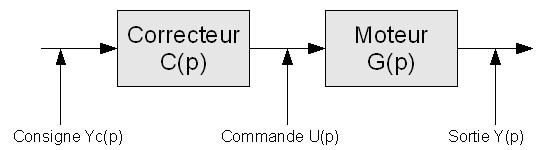
Lorsque les bloc sont en série comme ça, il est simple d'établir des équations entre les différents éléments, il suffit de les multiplier, par exemple, U(p) = Yc(p)*C(p), Y(p)=U(p)*G(p) donc
Y(p) = Yc(p)*C(p)*G(p). Un tel système est déjà capable de prendre en compte une consigne et de la répercuter correctement sur le moteur, il peut également améliorer la précision du moteur. Cependant, ce n'est pas encore vraiment le sujet de ce chapitre, c'est pour plus tard !
Voyons maintenant l'exemple d'un système bouclé.
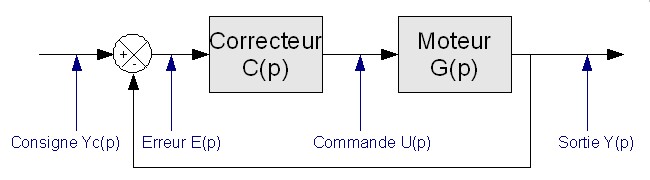
Sur ce système, il est nécessaire de regarder les signes indiqués dans le soustracteur/additionneur (boule avec la croix), un fil possède toujours le même signal tant qu'il ne rencontre pas d'élément. On peut écrire les équations suivantes : E(p) = Yc(p) – Y(p) , U(p) = E(p)*C(p) , Y(p) = G(p)*U(p) on à donc : Y(p) = (Yc(p) – Y(p))*C(p)*G(p), le but étant d'écrire les signaux d'entré et de sortie en fonction des éléments qui composent le système. L'intérêt d'un système bouclé comme celui-ci est de prendre en compte les perturbations que pourrait subir le moteur (pièces qui usent, freins ...) pour corriger et toujours tourner à la même vitesse quoi qu'il arrive.
 Attention ! C(p) et G(p) sont des fonctions de transfert mais les autres sont seulement des signaux exprimés en fonction de p.
Attention ! C(p) et G(p) sont des fonctions de transfert mais les autres sont seulement des signaux exprimés en fonction de p.
Voilà ce chapitre touche à sa fin, j'espère qu'il vous a donné un peu de baume au cœur pour trouver la force de continuer !
Performance d'une réponse
Nous allons avoir besoin de définir tout un tas de paramètres concernant le signal de sortie pour caractériser l'efficacité, l'attitude, les performances de la correction, de l'asservissement. Ce n'est pas très compliqué, c'est surtout de la lecture graphique (bien qu'il est possible de trouver ces paramètres par calcul aussi).
La stabilité
Comparons trois signaux de sortie différent que vous pourriez tout à fait rencontrer.

- Celui en rouge est instable (ou en limite de stabilité) car il oscille de façon continu.
- Celui en noir est stable mais pas très performant
- Celui en vert est stable et très performant, c'est ce vers quoi nous voulons arriver.
Comme notre but n'est pas de faire osciller notre moteur en le faisant tourner de droite à gauche ( bien qu'on puisse sûrement y trouver des applications ) , il faut que la réponse soit la plus stable possible.
La précision
Comparons deux signaux de sortie différent que vous pourriez tout à fait rencontrer par rapport au signal de commande, on suppose qu'on souhait commander identiquement le moteur dans les deux cas donc leur signal de commande (bleu) est identique.
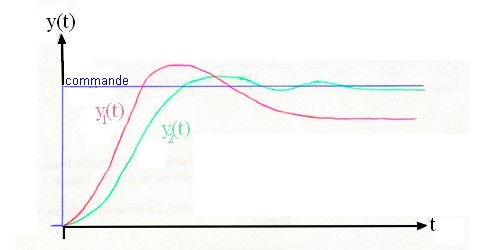
- Celui en rouge n'est pas précis, vers l'infinie, il ne superpose pas le signal de commande.
- Celui en vert est précis, vers l'infinie, il est confondu avec le signal de commande.
La rapidité
Comparons deux signaux de sortie différents par rapport au signal de commande identique dans les deux cas.
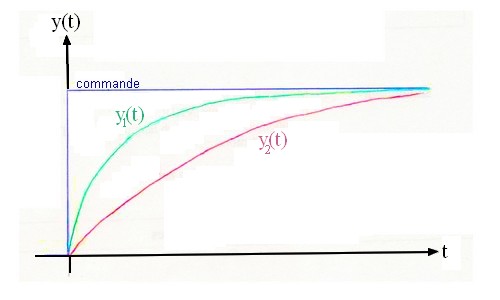
- Celui en rouge n'est pas rapide, il met du temps avant de se rapprocher du signal de commande.
- Celui en vert est plus rapide, il s'approche plus vite du signal de commande.
Voilà les trois facteurs qui décrivent les performances d'un asservissement, tout est histoire de compromis entre ces facteurs. Un système rapide aura malheureusement tendance à osciller, un système précis, lui aura tendance à être lent ... Rassurez vous, avec du bon matériel, on arrive à obtenir des performances presque parfaite, c'est a dire un signal de sortie qui recopie presque le signal de commande.
Voyons maintenant les notions un peu plus chiffrées pour décrire les performances d'un système.
Grandeurs de caractérisations
Nous allons maintenant voir toutes les grandeurs qui peuvent nous permettre d'exposer les caractéristiques d'une réponse. Ce chapitre va être exposé en deux parties, une partie pour les grandeurs qu'on lit sur la réponse en fonction du temps, et une seconde partie pour les grandeurs qu'on lit sur la réponse en fonction de la fréquence (diagramme de bode). Nous allons dans chaque cas distinguer si la réponse est d'ordre 1 ou d'ordre 2, nous n'étudierons pas l'ordre 3. De plus, les diagrammes de bode seront cette fois réel et non plus asymptotique.
Rappel ! Une réponse est d'ordre 1 si dans l'expression de celle-ci on trouve seulement du t pour le domaine temporel ou du p pour le domaine fréquentiel. Elle est d'ordre 2 si on trouve t et t au carré (ou seulement t au carré) dans le domaine temporel ou p et p au carré (ou seulement p au carré) dans le domaine fréquentiel.
La réponse en fonction du temps
Premier ordre
Le premier ordre est une fonction de transfert de la forme 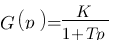 (comme le montage RC que nous avons vu précédemment)
(comme le montage RC que nous avons vu précédemment)
 Comment faire pour enregistrer un tel signal ?
Comment faire pour enregistrer un tel signal ?
On réalise le montage RC, on règle l'oscilloscope ( oui oui il faut être équipé et en plus encore faut-il que votre oscilloscope soit performant) en mode normal ou monocoup sur front montant (c'est à dire qu'il va commencer à enregistrer la tension lorsque qu'il aura détecter que la tension monte), branchez l'oscilloscope pour mesurer la tension de sortie du circuit RC, appliquez ensuite brutalement une tension d'entrée continue de 1V. Normalement, le tour est joué ! L'avantage de mettre une tension d'entrée de 1V est tout bête, vous voulez définir la fonction de transfert du circuit , celle-ci vaut 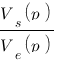 et donc si Ve(t) = 1 alors on a aussi Ve(p) = 1 ainsi G(p)=Vs(p), nous observons donc la réponse et la fonction de transfert en même temps puisque ceux-ci sont égaux !
et donc si Ve(t) = 1 alors on a aussi Ve(p) = 1 ainsi G(p)=Vs(p), nous observons donc la réponse et la fonction de transfert en même temps puisque ceux-ci sont égaux !
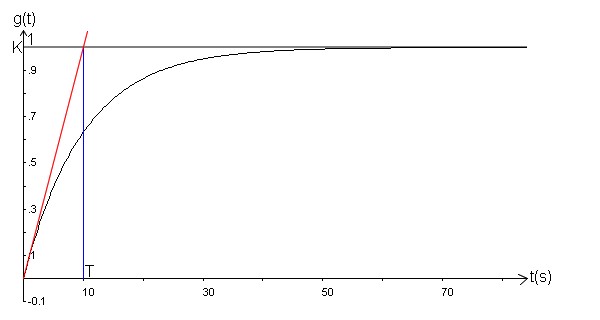
Retournons a nos moutons, en observant cette réponse à un échelon de 1V, on peut directement lire les deux variables qui définissent la fonction de transfert :
- K = la valeur maximum vers laquelle se rapproche la réponse (voir courbe, ici K=1)
- Pour T, c'est un tout petit peu plus compliqué, on trace l'asymptote oblique à t=0s (droite rouge) et on trace une droite verticale (droite bleu ) au niveau de l'intersection de l'asymptote avec la droite horizontale au niveau de K (ici droite grise qui est confondu avec le signal d'entrée), il n'y a plus qu'à lire sur l'axe de temps la valeur de T (voir courbe, ici T=10s)
La fonction de transfert correspondant à cette courbe est : 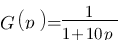
Deuxième ordre
Le deuxième ordre est de la forme 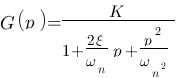 , nous avons vu précédemment un montage du deuxième ordre mais il ne correspond pas à cette forme-ci, cependant si nous mettions deux montages RC bout à bout alors le tout formerait un système du deuxième ordre applicable à ce modèle.
, nous avons vu précédemment un montage du deuxième ordre mais il ne correspond pas à cette forme-ci, cependant si nous mettions deux montages RC bout à bout alors le tout formerait un système du deuxième ordre applicable à ce modèle.
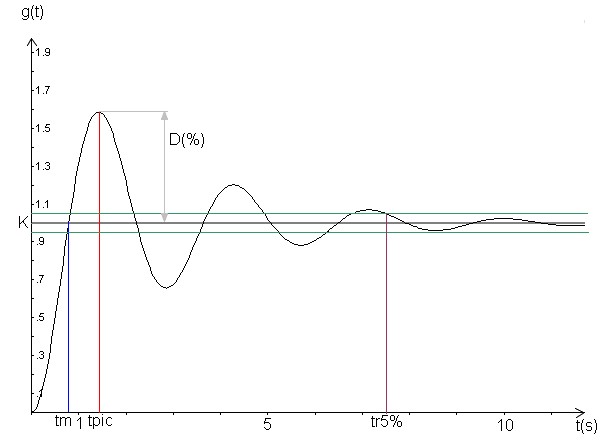
Dans ce cas, il n'y a que K que l'on peut lire facilement, K est encore une fois au niveau de la réponse en l'infinie, ici il vaut encore 1. Cependant, il est aisé d'estimer 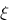 , ce nombre représente en fait le niveau de stabilité du système, si le système n'oscille peu ou pas alors
, ce nombre représente en fait le niveau de stabilité du système, si le système n'oscille peu ou pas alors 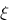 est grand, à l'inverse, si il y a beaucoup d'oscillations,
est grand, à l'inverse, si il y a beaucoup d'oscillations, 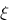 est faible, lorsque
est faible, lorsque 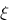 =0.7 alors on considère que le système est stable. Récapitulons sur ce que l'on peut estimer sur
=0.7 alors on considère que le système est stable. Récapitulons sur ce que l'on peut estimer sur 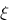 :
:
- 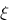 <0.7 : il y a beaucoup d'oscillations, le système est instable (c'est notre cas ici)
<0.7 : il y a beaucoup d'oscillations, le système est instable (c'est notre cas ici)
- 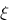 =0.7 : c'est LE chiffre parfait, le système est stable et rapide. (cf performance d'une réponse – stabilité – courbe verte)
=0.7 : c'est LE chiffre parfait, le système est stable et rapide. (cf performance d'une réponse – stabilité – courbe verte)
- 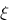 >0.7 : c'est très stable, ça c'est sûr ! Sûrement très lent aussi ... (cf performance d'une réponse – rapidité - courbe rouge)
>0.7 : c'est très stable, ça c'est sûr ! Sûrement très lent aussi ... (cf performance d'une réponse – rapidité - courbe rouge)
Les estimations à faire sur 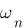 sont beaucoup moins évidente et clair.
sont beaucoup moins évidente et clair.
Comme nous pouvons pas avoir les valeurs exactes de 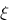 et
et 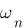 , il existe d'autre variables que l'on peut lire directement pour définir la réponse, étudions les !
, il existe d'autre variables que l'on peut lire directement pour définir la réponse, étudions les !
Au niveau de l'axe des temps, on définit trois caractéristiques :
-  : c'est le temps de montée ! C'est le temps que la réponse met pour atteindre sa valeur en l'infinie, sur le dessin, c'est la droite bleu qui le représente et il vaut environ 0,75 sec.
: c'est le temps de montée ! C'est le temps que la réponse met pour atteindre sa valeur en l'infinie, sur le dessin, c'est la droite bleu qui le représente et il vaut environ 0,75 sec.
- 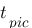 : c'est le temps où la réponse atteint son maximum, c'est la droite rouge :
: c'est le temps où la réponse atteint son maximum, c'est la droite rouge : 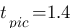
- 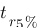 : c'est le temps de réponse à 5%, celui-ci est un peu plus compliqué, il représente le temps que la réponse met pour qu'elle ne dépasse plus sa valeur à l'infinie à plus ou moins 5%. La réponse vaut 1V à l'infinie donc traçons deux droites vertes à 0,95V et 1,05V qui représente les limites à ne plus dépasser. À partir de la droite violette, l'ensemble de la réponse reste entre les deux limites à + ou – 5% établi donc c'est ici que se situe
: c'est le temps de réponse à 5%, celui-ci est un peu plus compliqué, il représente le temps que la réponse met pour qu'elle ne dépasse plus sa valeur à l'infinie à plus ou moins 5%. La réponse vaut 1V à l'infinie donc traçons deux droites vertes à 0,95V et 1,05V qui représente les limites à ne plus dépasser. À partir de la droite violette, l'ensemble de la réponse reste entre les deux limites à + ou – 5% établi donc c'est ici que se situe 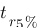 ,
, 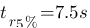 . De même, on peut définir
. De même, on peut définir 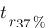 , le temps de réponse à 37%.
, le temps de réponse à 37%.
Au niveau de l'axe des tensions, on définit une caractéristique :
- D(%) : c'est le dépassement, il est représenté par la flèche grise et se calcul simplement comme ceci : 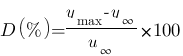 , ici on a : y_max = 1.6V et y_infty = 1V donc
, ici on a : y_max = 1.6V et y_infty = 1V donc 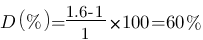 . Un dépassement de 60% est assez élevé !
. Un dépassement de 60% est assez élevé !
Information complémentaire : grâce à ces quartes caractéristiques on peut calculer simplement xi et omega_n . Il existe un tableau tout prêt qui nous livre ces calculs presque tout prêt servi sur un plateau. Nous reverrons ceci plus tard.
La réponse en fonction de la fréquence
Premier ordre
Revenons à un montage du 1er ordre, de la forme 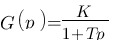 , qui a comme diagramme de bode (gain) la figure suivante.
, qui a comme diagramme de bode (gain) la figure suivante.
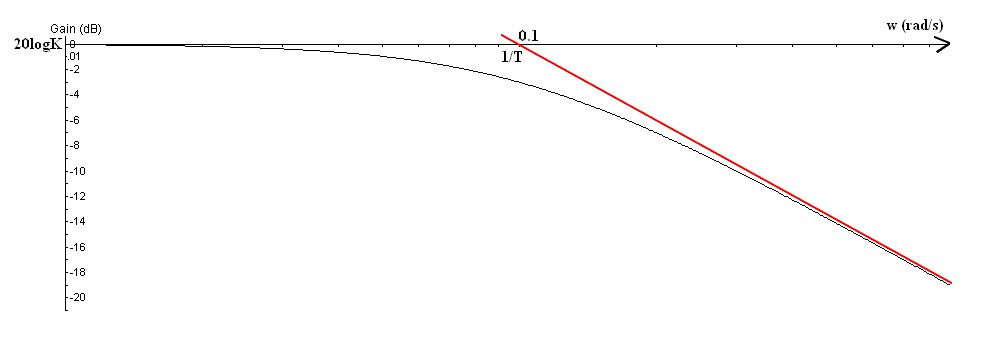
Ici, c'est simple, on peut lire quasiment directement sur la phase les inconnues K et T contre un peu de math. Lorsque la fréquence est faible ( donc w aussi ) , alors le gain vaut 20 log K donc, pour un gain à fréquence très faible : 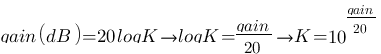 , ici le gain vaut 0 pour des fréquences très faible donc
, ici le gain vaut 0 pour des fréquences très faible donc 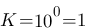 . Pour T, il faut tracer l'asymptote pour les fréquences très grandes (courbe rouge) alors au point d'intersection entre cette asymptote et l'axe des abscisse on a :
. Pour T, il faut tracer l'asymptote pour les fréquences très grandes (courbe rouge) alors au point d'intersection entre cette asymptote et l'axe des abscisse on a : 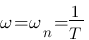 , on note donc
, on note donc 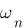 ce point assez particulier. Ici,
ce point assez particulier. Ici, 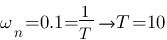 . On retrouve les même résultats que pour l'étude temporelle, logique j'ai choisie la même fonction de transfert pour tracer les deux courbes.
. On retrouve les même résultats que pour l'étude temporelle, logique j'ai choisie la même fonction de transfert pour tracer les deux courbes.
Deuxième ordre
Ah, celui-ci est toujours plus compliqué que le 1er ordre, et malheureusement il est plus réaliste que le 1er ordre ! Allez, toujours la même fonction de transfert de type 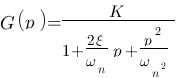 , l'étude de celle-ci en fréquence nous donne le résultat suivant (seulement le gain car il est porteur de beaucoup plus d'information), malheureusement ce diagramme aura son abscisse gradué en fonction de la fréquence et non de la pulsation, tant pis, ça vous fera de l'exercice !
, l'étude de celle-ci en fréquence nous donne le résultat suivant (seulement le gain car il est porteur de beaucoup plus d'information), malheureusement ce diagramme aura son abscisse gradué en fonction de la fréquence et non de la pulsation, tant pis, ça vous fera de l'exercice !
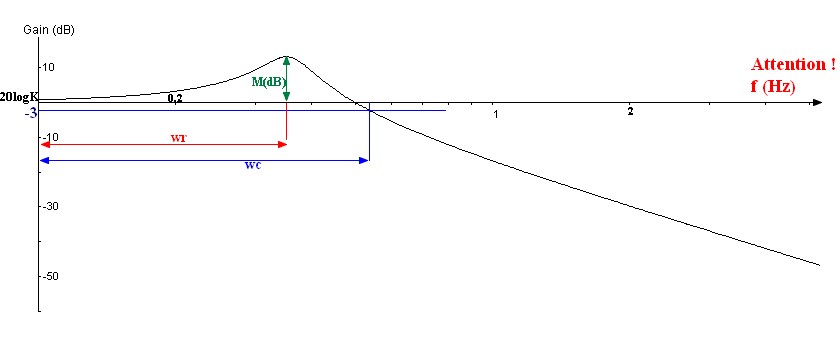
- K : c'est la même chose que pour le 1er ordre.
- 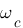 : c'est la pulsation lorsque le gain est 3dB en dessous de sa valeur pour des fréquences faibles (flêche bleu), ici
: c'est la pulsation lorsque le gain est 3dB en dessous de sa valeur pour des fréquences faibles (flêche bleu), ici 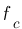 est compris entre 0,5 et 0,6 rad/s donc
est compris entre 0,5 et 0,6 rad/s donc 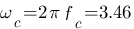 rad/s.
rad/s.
- 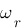 : c'est la pulsation lorsque le gain est maximum (flèche rouge), ici
: c'est la pulsation lorsque le gain est maximum (flèche rouge), ici 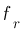 est compris entre 0,3 et 0,4 rad/s donc
est compris entre 0,3 et 0,4 rad/s donc 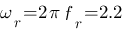 rad/s.
rad/s.
M(dB) : c'est la valeur du gain lorsqu'il est maximum (flèche verte), ici M(dB) = 11dB environ.
Voilà ce chapitre touche à sa fin, vous êtes maintenant prêt à utiliser toutes ces grandeurs barbares ! Vous aurez peut être remarqué que les graphiques ne permettent pas de retrouver les éléments des fonctions de transfert lorsque celles-ci sont du deuxième ordre, nous allons donc dans le chapitre suivant voir comment retrouver ces éléments à partir des grandeurs de caractérisations que nous avons introduit dans ce chapitre, vous allez voir ce n'est pas du tout compliqué, c'est juste de la lecture de tableau et une division !
Tableau de correspondance
Ce chapitre va être court et simple ! Remerciez vos prédécesseurs qui ont préparés tout les résultats dans un jolie tableau où vous n'aurez qu'à piocher ce que vous avez besoin !
On va donc voir comment lier les grandeurs caractéristiques de second ordre du chapitre précédent 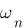 à et
à et 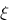 . Je vous rappelle la forme de la fonction de transfert d'un système du deuxième ordre :
. Je vous rappelle la forme de la fonction de transfert d'un système du deuxième ordre : 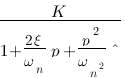 . Vous aller pouvoir calculer
. Vous aller pouvoir calculer 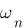 et
et 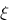 connaissant certaines de ces grandeurs :
connaissant certaines de ces grandeurs : 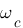 ,
, 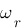 , M(dB),
, M(dB),  ,
, 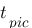 ,
, 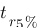 en vous référant à ce tableau :
en vous référant à ce tableau :
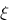 |
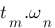 |
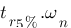 |
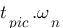 |
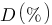 |
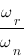 |
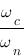 |
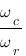 |
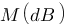 |
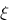 |
| 0.1 | 1.68 | 30 | 3.16 | 73 | 0.99 | 1.54 | 1.56 | 14 | 0.1 |
| 0.15 | 1.74 | 20 | 3.18 | 62 | 0.98 | 1.53 | 1.56 | 10.5 | 0.15 |
| 0.2 | 1.81 | 14 | 3.21 | 53 | 0.96 | 1.51 | 1.57 | 8.1 | 0.2 |
| 0.25 | 1.88 | 11 | 3.24 | 44 | 0.94 | 1.48 | 1.59 | 6.3 | 0.25 |
| 0.3 | 1.97 | 10.1 | 3.29 | 37 | 0.91 | 1.45 | 1.61 | 4.8 | 0.3 |
| 0.35 | 2.06 | 7.9 | 3.35 | 31 | 0.87 | 1.42 | 1.63 | 3.6 | 0.35 |
| 0.4 | 2.16 | 7.7 | 3.43 | 25 | 0.82 | 1.37 | 1.67 | 2.7 | 0.4 |
| 0.45 | 2.28 | 5.4 | 3.52 | 21 | 0.77 | 1.33 | 1.72 | 1.9 | 0.45 |
| 0.5 | 2.42 | 5.3 | 3.63 | 16 | 0.71 | 1.27 | 1.80 | 1.2 | 0.5 |
| 0.55 | 2.58 | 5.3 | 3.76 | 12.6 | 0.63 | 1.21 | 1.93 | 0.7 | 0.55 |
| 0.6 | 2.77 | 5.2 | 3.93 | 9.5 | 0.53 | 1.15 | 2.17 | 0.3 | 0.6 |
| 0.65 | 3.00 | 5.0 | 4.13 | 6.8 | 0.39 | 1.08 | 2.74 | 0.1 | 0.65 |
| 0.707 | 3.29 | 3.0 | 4.4 | 4.6 | 0 | 1 | 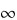 |
0 | 0.707 |
| 0.75 | 3.66 | 3.1 | 4.75 | 2.84 | 0.94 | 0.75 | |||
| 0.8 | 4.16 | 3.4 | 5.24 | 1.52 | 0.87 | 0.8 | |||
| 0.85 | 4.91 | 3.7 | 5.96 | 0.63 | 0.81 | 0.85 | |||
| 0.9 | 6.17 | 4 | 7.21 | 0.15 | 0.75 | 0.9 | |||
| 0.95 | 9.09 | 4.1 | 10.06 | 0.01 | 0.69 | 0.95 | |||
| 1 | 4.8 | 0.64 | 1 | ||||||
| 1.25 | 6.6 | 0.47 | 1.25 | ||||||
| 1.5 | 8.2 | 0.37 | 1.5 | ||||||
| 1.75 | 9.9 | 0.31 | 1.75 | ||||||
| 2 | 11.4 | 0.27 | 2 | ||||||
| 2.25 | 13 | 0.23 | 2.25 |
Bon bah voilà c'est fini ! ![]() Ça fait vraiment cours quand même, let's see un exemple ! Reprenons les lectures graphiques vu précédemment :
Ça fait vraiment cours quand même, let's see un exemple ! Reprenons les lectures graphiques vu précédemment :
- Dans un premier temps sur la courbe en fonction du temps, on avait D(%) = 60 % donc 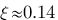 (ouuu ça oscille !), on avait
(ouuu ça oscille !), on avait 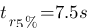 et je peux lire dans le tableau, en gros,
et je peux lire dans le tableau, en gros, 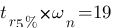 pour un
pour un 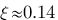 donc
donc 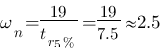 rad/s, le tour est joué !
rad/s, le tour est joué !
- Dans un second temps, sur le diagramme de bode, on avait M(dB) = 11 dB donc 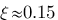 , on avait
, on avait 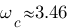 et on lit sur le tableau que
et on lit sur le tableau que 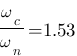 donc
donc 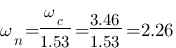 rad/s . Ouf on retrouve à peu prêt la même chose aux erreurs de tracé et de lecture prêt !
rad/s . Ouf on retrouve à peu prêt la même chose aux erreurs de tracé et de lecture prêt ! ![]()
A utiliser sans modération !
Asservissement de vitesse
Correcteur proportionnel BO
Maintenant que nous possédons tout les outils nécessaires à l'étude des asservissements, il ne reste plus qu'à les étudier ! Commençons simplement par un correcteur proportionnel en boucle ouverte. On va étudier un système, sur lequel on installe un correcteur censé améliorer le fonctionnement de ce système. On sous-entend que grâce au correcteur, le système pourra recopier au mieux possible la consigne que l'on souhaiterait que notre système suive.
Étude Théorique
Pour simplifier cette entrée en matière dans le monde des correcteurs, on va utiliser un système (moteur par exemple) que l'on va considérer d'ordre 1. De plus, on veux faire de l'asservissement de vitesse. D'après ces 2 données on peut dire que : 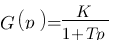 . En réalité, les systèmes sont mieux décris quand ils le sont par une fonction de transfert d'ordre 2, on va donc démarrer doucement par un ordre 1 et puis dans les chapitres suivants, on introduira un exemple avec un système d'ordre 2.
. En réalité, les systèmes sont mieux décris quand ils le sont par une fonction de transfert d'ordre 2, on va donc démarrer doucement par un ordre 1 et puis dans les chapitres suivants, on introduira un exemple avec un système d'ordre 2.
Le correcteur proportionnel est un simple correcteur de gain Kc. Voici le schéma du système :
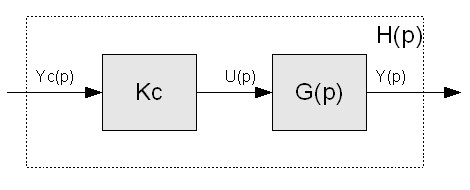
Une fois le schéma établi, l'étude consiste d'abord à chercher la fonction de transfert du système correspondant complet :
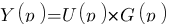
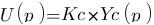
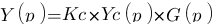
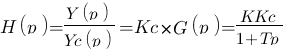
Maintenant que nous avons la fonction de transfert, traçons le diagramme de bode correspondant. Pour le tracer, je rappelle qu'il faut remplacer "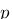 par "
par "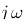 ", soit :
", soit : 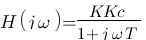 , on reconnait cette fonction dans les diagrammes référents vu précédemment :
, on reconnait cette fonction dans les diagrammes référents vu précédemment :
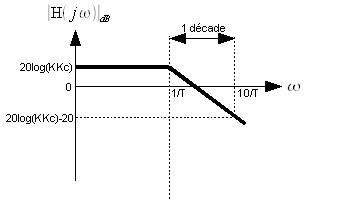
En utilisant la fonction de transfert, le diagramme de bode, on peut retrouver la réponse en fonction du temps du système. Si on applique un échelon d'amplitude 0.5V à l'entrée de ce système, avec Kc=2, K=1, on obtiendrait la réponse de ce système dans le temps suivante :
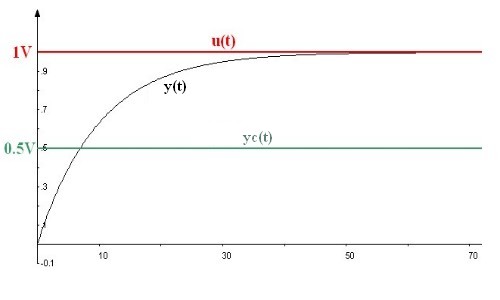
On a 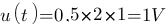 .
.
 On en tire quoi de cette étude théorique ?
On en tire quoi de cette étude théorique ?
Pas terrible comme réponse vous ne trouvez pas ? On a donner à notre système une consigne claire, "1V TOUT DE SUITE MAINTENANT", mais ce fainéant de moteur met du temps à atteindre la consigne indiquée ! On peut avouer qu'on a rien amélioré du tout , c'est pas avec ça qu'on va faire des choses précises nets et claires. Quoi qu'il en soit, maintenant on sait au moins comment corriger une commande, le 0.5V qui correspond à la commande, envoyé au système, se traduit en 1V qui correspond à la consigne.
Etude Pratique
 Et avec des composants, un correcteur proportionnel ça ressemble à quoi ?
Et avec des composants, un correcteur proportionnel ça ressemble à quoi ?
Voici deux schémas d'amplificateur, ce qui correspond à un correcteur proportionnel :
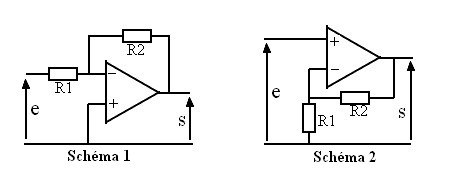
Fonction de transfert du schéma 1 : 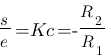
Fonction de transfert du schéma 2 : 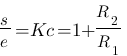
Voilà, chacun des deux montages a son charme, le premier inverse au passage la tension - il y a un petit "-" dans la fonction de transfert - mais peut atténuer la tension (efficace) |Kc| < 1 ou |Kc| > 1, le second ne sait qu'amplifier (Kc > 1) mais n'inverse pas la tension. Il peut être également très intéressant de remplacer une résistance de ce correcteur par un potentiomètre pour avoir un Kc réglable !
Voilà un peu le montage du montage :
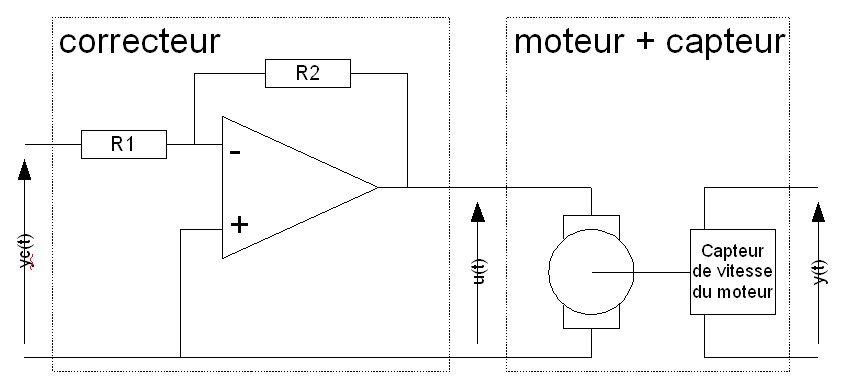
Comprennez bien ici que le capteur de vitesse du moteur n'est absolument pas nécessaire, à part pour regarder ce qu'il se passe ! ![]() Dans tout les montages en boucle ouverte, c'est le cas, on n'utilise pas le signal du capteur. Par contre, dans le cas des boucles fermées, ce capteur prend toute son importance, et c'est là qu'on va faire de la vrai régulation.
Dans tout les montages en boucle ouverte, c'est le cas, on n'utilise pas le signal du capteur. Par contre, dans le cas des boucles fermées, ce capteur prend toute son importance, et c'est là qu'on va faire de la vrai régulation.
Ce n'est pas un système très intéressant, il n'apporte par grand chose si ce n'est que la sortie est amplifiée de Kc à l'infinie mais elle n'est nullement améliorée d'un point de vue stabilité, rapidité, précision. On va donc rapidement passer à un système bouclé ! Quelque chose de performant et de merveilleux !
Correcteur proportionnel BF
Dans ce chapitre, nous allons effectuer les même démarches que dans le chapitre précédent. De plus, on va reprendre le même correcteur proportionnel, toujours en asservissement de vitesse, sauf que cette fois-ci nous allons refermer la boucle !
Etude Théorique
On continue à faire un asservissement de vitesse et à utiliser un système d'ordre 1, on a donc : 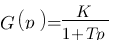 . Le correcteur proportionnel est toujours un simple correcteur de gain Kc. On lui ajoute une boucle. Voici donc le schéma du système muni de son correcteur proportionnel, en boucle fermé:
. Le correcteur proportionnel est toujours un simple correcteur de gain Kc. On lui ajoute une boucle. Voici donc le schéma du système muni de son correcteur proportionnel, en boucle fermé:
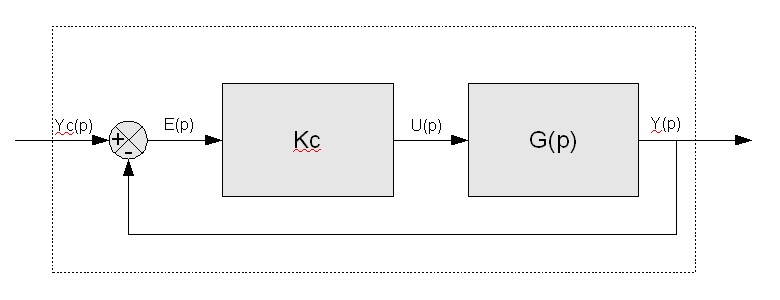
On recherche la fonction de transfert du système correspondant :
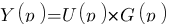
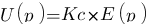
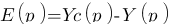
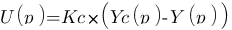
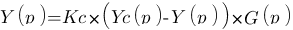
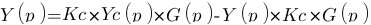
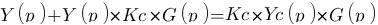
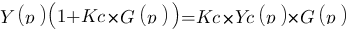
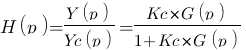
Piouf voilà, la première étape du calcul est faite ! En fait, avec un peu d'expérience on sait tout de suite qu'en boucle ouverte c'est toujours de cette forme là :  ! Il fallait bien que je vous fasse la démonstration au moins une fois
! Il fallait bien que je vous fasse la démonstration au moins une fois ![]() .
.
Remplaçons maintenant G(p):
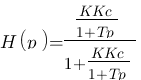 (Trop d'étages à mon gout
(Trop d'étages à mon gout ![]() , on multiplie en haut et en bas par
, on multiplie en haut et en bas par 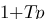 )
)
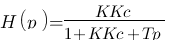 Ouf nous y voilà enfin ! Faux espoirs
Ouf nous y voilà enfin ! Faux espoirs ![]() c'est pas sous une forme très conventionnel ça !
c'est pas sous une forme très conventionnel ça !
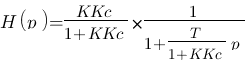 Maintenant on y est ! Ca parait plus compliqué comme ça mais en fait ça ne l'est pas. Si si je vous assure :| , en fait la forme conventionnel d'une fonction de transfert de premier ordre comme celle-ci c'est
Maintenant on y est ! Ca parait plus compliqué comme ça mais en fait ça ne l'est pas. Si si je vous assure :| , en fait la forme conventionnel d'une fonction de transfert de premier ordre comme celle-ci c'est 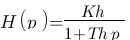 . J'ai donné des noms différents aux K et T car sinon on va s'y perdre. On a donc
. J'ai donné des noms différents aux K et T car sinon on va s'y perdre. On a donc 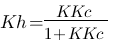 et
et 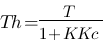 . Ne vous mélenagez pas dans les K et les T sinon ça vire à la pagaille
. Ne vous mélenagez pas dans les K et les T sinon ça vire à la pagaille ![]() (comment ça ça l'est déjà o_O ). Récapitulons qui appartient à quoi
(comment ça ça l'est déjà o_O ). Récapitulons qui appartient à quoi
K : le K de la fonction de transfert du moteur+capteur.
Kc : le K de la fonction de transfert du correcteur.
Kh : le K de la fonction de transfert de l'ensemble du système.
T : le T de la fonction de transfert du moteur+capteur.
Th : le T de la fonction de transfert de l'ensemble du système.
Voilà, j'espère que pour vous tout est bien clair maintenant.
Maintenant que nous avons la fonction de transfert, traçons le diagramme de bode correspondant. Pour le tracer, je rappelle qu'il faut remplacer "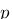 " par "
" par "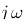 ", soit :
", soit : 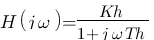 , c'est exactement la même fonction de transfert qu'en boucle ouverte aux coefficient prêt !!! Cool on a fini on se barre !!!
, c'est exactement la même fonction de transfert qu'en boucle ouverte aux coefficient prêt !!! Cool on a fini on se barre !!!
Vous avez tout à fait raison, c'est la même chose donc on ne va pas afficher le diagramme de bode. MAIS... il y a tout de même une belle différence ! Cette différence réside dans les coefficients Kh et Th.
Le graphique en fonction du temps, ça donne ça (rappellez vous de ce qu'on a vu précédemment) :
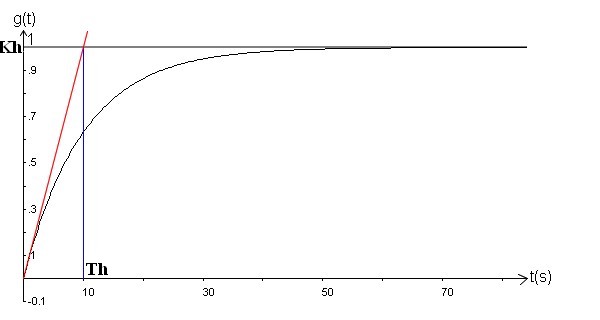
Bon par rapport à Kh, il n'y a rien d'interessant à dire par rapport à son effet sur la performance de la réponse.
Mais Th, lui, il joue tout son rôle, on a vu que 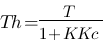 . Là, on s'aperçoit que plus Kc est grand et plus Th est petit ! (Je ne parle pas de K car on ne peut pas jouer là dessus mais le Kc par contre on en fait tout ce qu'on en veut). Imaginer donc le même graphique mais avec un Kc très grand donc un Th très faible ! Voilà ce que ça pourrait donner :
. Là, on s'aperçoit que plus Kc est grand et plus Th est petit ! (Je ne parle pas de K car on ne peut pas jouer là dessus mais le Kc par contre on en fait tout ce qu'on en veut). Imaginer donc le même graphique mais avec un Kc très grand donc un Th très faible ! Voilà ce que ça pourrait donner :
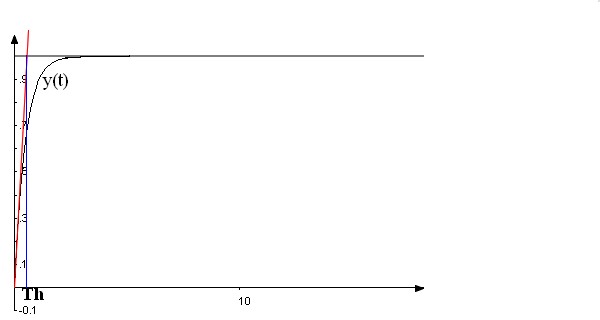
y(t) recopie presque la commande ! C'est merveilleux, et si Th était nul alors la régulation serait parfaite ! J'ai plus rien de plus à vous dire sur les correcteurs alors ! Enfin ... il faut revenir sur terre, un Th nul équivaut à un Kc infini, la nature elle aime vraiment pas l'infini. Comment oseriez vous concevoir un amplificateur de gain infini ?
Un second problème apparait avec ce montage, rappelez vous, 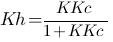 , on ne peut pas jouer sur K, il est fixé par la système, à 1 par exemple, imaginons que nous mettons comme commande à l'entré de notre système 1V également. On souhaiterais donc que Kh=1 pour recopier l'entrée, cependant l'équation
, on ne peut pas jouer sur K, il est fixé par la système, à 1 par exemple, imaginons que nous mettons comme commande à l'entré de notre système 1V également. On souhaiterais donc que Kh=1 pour recopier l'entrée, cependant l'équation 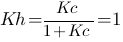 n'a pas de solution, encore une fois il faudrait également un Kc infinie pour obtenir Kh=1 ... On ne peut donc pas avoir une sortie qui recopie une entrée toute pile, en réalité ça donnerait quelque chose comme ça (avec un Kc assez grand tout de même) :
n'a pas de solution, encore une fois il faudrait également un Kc infinie pour obtenir Kh=1 ... On ne peut donc pas avoir une sortie qui recopie une entrée toute pile, en réalité ça donnerait quelque chose comme ça (avec un Kc assez grand tout de même) :
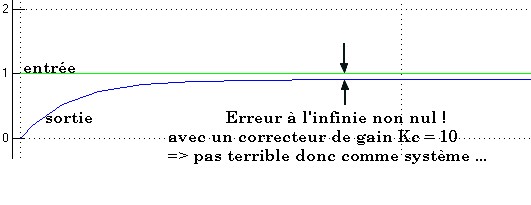
C'est tout le problème de ce montage, quoi qu'il en soit, avec celui-ci on peut vraiment avoir un résultat satisfaisant (presque...), mais rassurez vous, il existe d'autre système qui n'ont pas ces inconvéniants.
Correction des perturbations
Ce système corrige les perturbations, imaginez que vous venez embêter votre moteur en lui imposant un frein par exemple, le système va donc prendre en compte ce frein, mettre un peu plus de puissance en commande pour corriger la perturbation et toujours aller à la même vitesse malgré le frein.
Voici le schéma de la situation :

P(p) est la fonction de transfert de la perturbation, elle va donc s'ajouter (ou s'enlever si négatif) à la vitesse de rotation du moteur. Le capteur de vitesse Y(p) va constater cette perturbation, celle-ci est alors rebouclée par l'intermédiaire de l'erreur E(p) qui est corrigée par le correcteur Kc qui créer un signal de commande U(p) renvoyé dans le système G(p).
Voici les courbes illustrant une perturbation corrigée :

On peut constater toujours les soucis d'erreur à l'infini, mais la perturbation est grossièrement corrigée, vous pourrez toujours empècher le système de tourner, il sera plus têtu que vous !! A moins de tout faire fumer ...
Étude Pratique
Le correcteur c'est le même que vu précédemment. Le moteur et son capteur aussi. Il reste un petit élément à éclaircir, créer la boucle.
Voyons comment créer l'élément suivant : 
Ça s'appelle un soustracteur, et par chance c'est pas très dur à créer ! Voici le schéma d'un soustracteur :
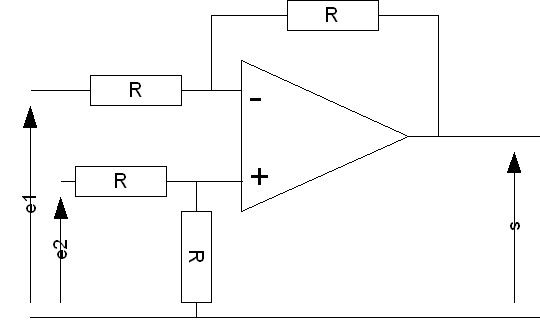
On a s = e2 - e1 si les quatre résistances sont identiques.
Il ne reste plus qu'à mettre tout ça bout à bout et le tour est joué !

Nous pouvons être fier de notre premier vrai asservissement/régulation, cependant ce système possède encore des défauts que nous tâcherons de résoudre avec d'autres correcteurs plus compliqués dans les prochains chapitres.
Correcteur proportionnel-dérivée
On poursuit avec un nouvel exemple de correcteur : le correcteur PD Proportionnel-Dérivé. Celui-ci est toujours plus performant que les précédents et est inséré dans une boucle fermée.
Etude Théorique
Le schéma du correcteur PD commence à se compliquer un petit peu :
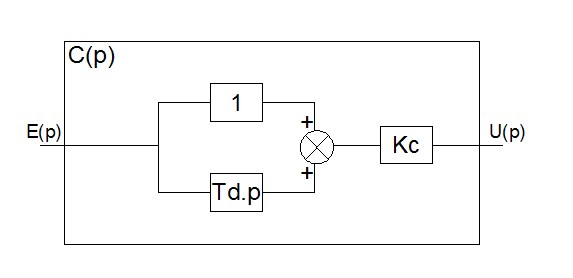
Recherchons la fonction de transfert 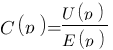 de ce correcteur PD :
de ce correcteur PD :
E(p) est d'abord multiplier par deux module 1 et Tdp additionnés, puis ensuite, multiplié par Kc. On a donc : 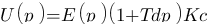 soit :
soit : 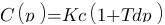 .
.
Reprenons un schéma globale du système avec un G(p) d'asservissement de vitesse d'ordre 1, soit 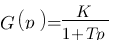
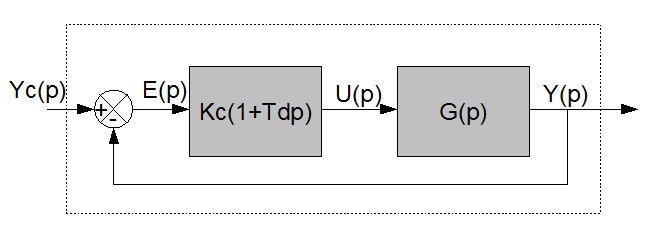
Comme d'habitude, on va chercher la fonction de transfert générale H(p) du système :
On ne refait pas tout, on sait qu'on a le résultat suivant : 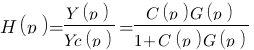
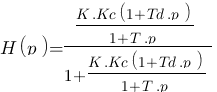
On multiplie en haut et ne bas par 1+T.p : 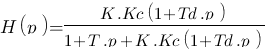
On simplifie le dénominateur : 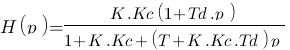
On met sous forme conventionnelle : 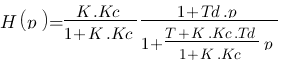
Voilà ! Il n'y a plus qu'à identifier les Kh, Th1 et Th2 de notre fonction 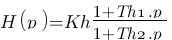 :
:
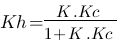
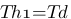
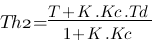
Traçons maintenant les graphiques correspondant pour se rendre compte du fonctionnement du système. En avant première, j'ai décidé de vous dévoilez comment je ponds ces graphiques ! Il suffit d'utiliser le logiciel payant de mathématiques Matlab. Ce logiciel est très performant, très utilisé, mais très cher aussi... Il intègre un module qui porte le nom de "simulink" permettant de simuler des systèmes physique comme des systèmes électronique. Voici notre système Proportionnel-Dérivé sous simulink :
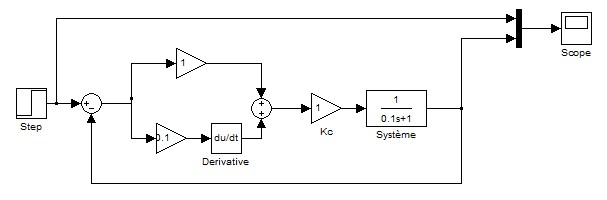
Vous devirez reconnaitre chacun de nos éléments, à quelques nuances prêts :
- la source n'est plus Yc(p) mais un vulgaire signal qui vaut toujours 1 au cours du temps à partir de t=0
- le "p" de "Tdp" est devenu un dérivateur, en effet, p est équivalent dans le temps à un dérivateur (d'oû le nom du correcteur par ailleurs), sinon ici Td=0,1.
- pour finir, le scope qui nous permet d'avoir nos signaux !
Voici les signaux obtenues pour Td=0.1, Kc=1 :
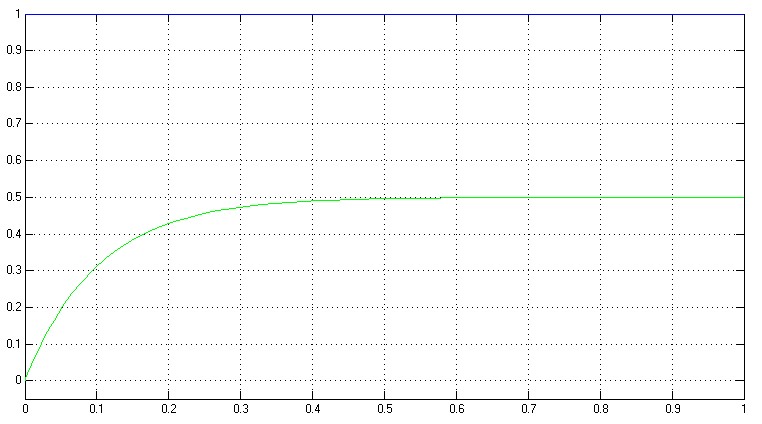
Qu'est ce que nous apporte ce correcteur ? A priori pas grand chose. Grosse erreur à l'infinie, lenteur ... Essayons de jouer sur les paramètres de notre correcteur, voici ce que l'on obtient pour Td=0,001 et Kc=20 :
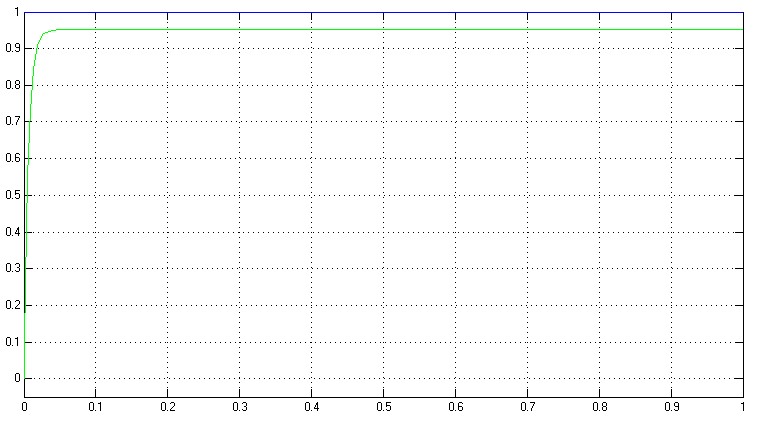
Quelle performance ! Le système est beaucoup plus rapide, l'erreur à l'infinie faible, mais toujours pas nulle ... Il faudrait en fait un Kc infini pour ne pas avoir d'erreur à l'infinie, ce qui est évidemment toujours impossible.
Intéressons nous maintenant aux perturbations, petite piqure de rappel sur la façon de modéliser une perturbation :
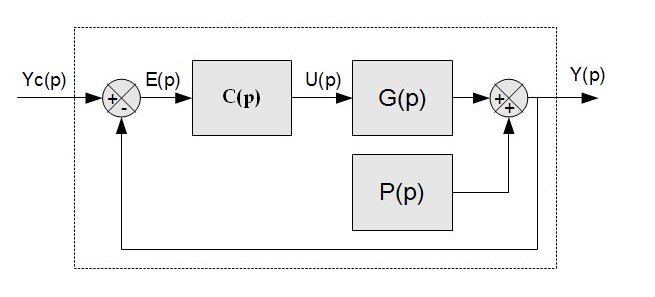
Sous simulink, on la simule de la manière suivante :
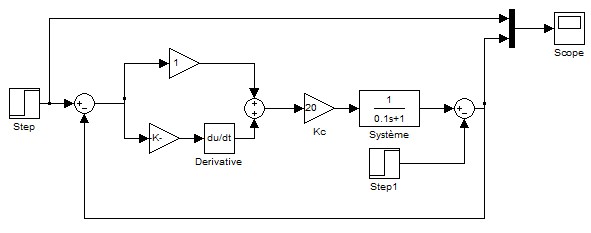
Notre petit système va avoir le droit à un sérieux coup de frein de 1 à partir de 0.5s, et voici le résultat :
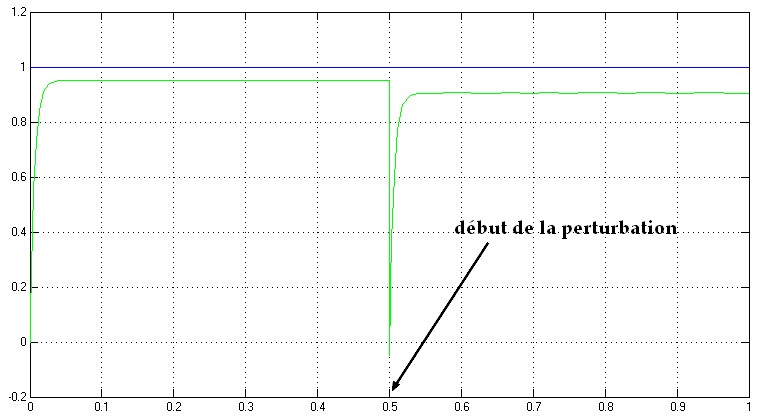
Que nenni ! Le vaillant correcteur encaisse plutôt bien le choc ...
Pas d'étude pratique pour ce correcteur étant donné que c'est approximativement là même chose que vu précédemment. Il est cependant aisé de trouver le schéma électronique sur internet d'un dérivateur. On verra dans un chapitre suivant comment faire un correcteur PID, qui est plus performant que le PD.
Ce qu'il va falloir retenir de ce chapitre, c'est que la composante "dérivée" d'un correcteur permet d'augmenter la rapidité du système. De plus, si on avait utilisé un système d'ordre 2 au lieu d'un système d'ordre 1 pour simuler notre moteur, on se serait rendu compte que la composante "dérivée" amène également beaucoup d'instabilités. Le système d'ordre 2 étant plus proche de la réalité que le système d'ordre 1.Rappel sur les notions d'ordre du système.
Vous savez également maintenant comment on peut simuler les systèmes à l'aide d'un ordinateur, mais pour ça il va falloir se procurer matlab et apprendre à s'en servir même si celui-ci n'est pas très compliqué.
Maintenant, place au correcteur proportionnel-intégrale, en y ajoutant une petite nouveauté, on va utiliser cette fois un système d'ordre 2 !
Annexes
Tableau de Laplace
| Domaine fréquentiel (Laplace) | Domaine temporel |
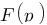 |
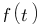 |
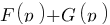 |
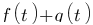 |
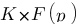 |
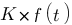 |
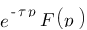 |
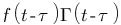 |
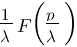 |
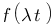 |
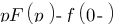 |
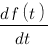 |
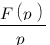 |
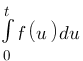 |
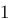 |
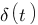 |
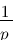 |
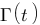 |
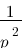 |
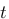 |
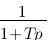 |
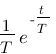 |
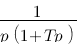 |
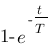 |
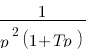 |
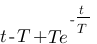 |
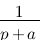 |
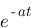 |
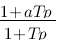 |
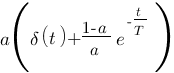 |
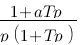 |
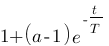 |
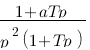 |
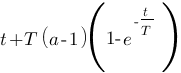 |
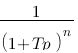 |
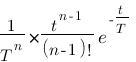 |
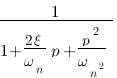 |
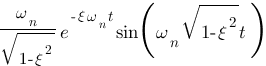 |
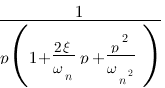 |
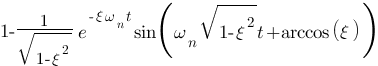 |
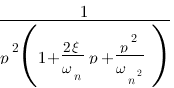 |
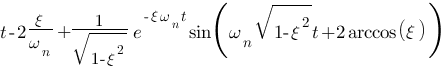 |
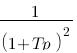 |
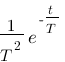 |
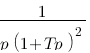 |
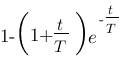 |
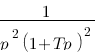 |
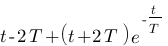 |
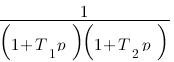 |
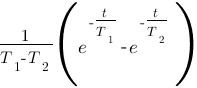 |
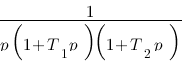 |
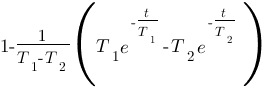 |
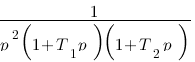 |
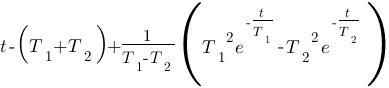 |
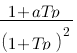 |
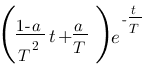 |
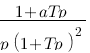 |
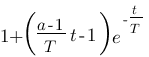 |
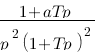 |
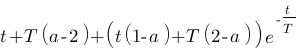 |
Modèles de correcteurs
Correcteurs proportionnels "P"

Fonction de transfert du schéma 1 : 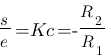
Fonction de transfert du schéma 2 : 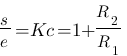
Avantages :
- Simplicité des montages
Inconvénients :
- Manque de rapidité
Tableau de correspondance
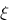 |
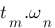 |
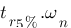 |
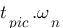 |
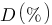 |
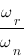 |
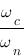 |
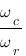 |
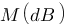 |
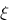 |
| 0.1 | 1.68 | 30 | 3.16 | 73 | 0.99 | 1.54 | 1.56 | 14 | 0.1 |
| 0.15 | 1.74 | 20 | 3.18 | 62 | 0.98 | 1.53 | 1.56 | 10.5 | 0.15 |
| 0.2 | 1.81 | 14 | 3.21 | 53 | 0.96 | 1.51 | 1.57 | 8.1 | 0.2 |
| 0.25 | 1.88 | 11 | 3.24 | 44 | 0.94 | 1.48 | 1.59 | 6.3 | 0.25 |
| 0.3 | 1.97 | 10.1 | 3.29 | 37 | 0.91 | 1.45 | 1.61 | 4.8 | 0.3 |
| 0.35 | 2.06 | 7.9 | 3.35 | 31 | 0.87 | 1.42 | 1.63 | 3.6 | 0.35 |
| 0.4 | 2.16 | 7.7 | 3.43 | 25 | 0.82 | 1.37 | 1.67 | 2.7 | 0.4 |
| 0.45 | 2.28 | 5.4 | 3.52 | 21 | 0.77 | 1.33 | 1.72 | 1.9 | 0.45 |
| 0.5 | 2.42 | 5.3 | 3.63 | 16 | 0.71 | 1.27 | 1.80 | 1.2 | 0.5 |
| 0.55 | 2.58 | 5.3 | 3.76 | 12.6 | 0.63 | 1.21 | 1.93 | 0.7 | 0.55 |
| 0.6 | 2.77 | 5.2 | 3.93 | 9.5 | 0.53 | 1.15 | 2.17 | 0.3 | 0.6 |
| 0.65 | 3.00 | 5.0 | 4.13 | 6.8 | 0.39 | 1.08 | 2.74 | 0.1 | 0.65 |
| 0.707 | 3.29 | 3.0 | 4.4 | 4.6 | 0 | 1 | 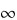 |
0 | 0.707 |
| 0.75 | 3.66 | 3.1 | 4.75 | 2.84 | 0.94 | 0.75 | |||
| 0.8 | 4.16 | 3.4 | 5.24 | 1.52 | 0.87 | 0.8 | |||
| 0.85 | 4.91 | 3.7 | 5.96 | 0.63 | 0.81 | 0.85 | |||
| 0.9 | 6.17 | 4 | 7.21 | 0.15 | 0.75 | 0.9 | |||
| 0.95 | 9.09 | 4.1 | 10.06 | 0.01 | 0.69 | 0.95 | |||
| 1 | 4.8 | 0.64 | 1 | ||||||
| 1.25 | 6.6 | 0.47 | 1.25 | ||||||
| 1.5 | 8.2 | 0.37 | 1.5 | ||||||
| 1.75 | 9.9 | 0.31 | 1.75 | ||||||
| 2 | 11.4 | 0.27 | 2 | ||||||
| 2.25 | 13 | 0.23 | 2.25 |














