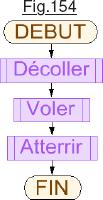
L’intégralité des logiciels actuels utilisent des sous-programmes. On peut concevoir des « subroutines » qui ne sont invoquées qu’une seule fois. Le but consiste à traiter dans des « blocs » faciles à identifier des séquences spécifiques. Par exemple le programme de la Fig.154 a été conçu en trois blocs qui sont invoqués les uns après les autres. Si l’on choisit avec pertinence les identificateurs des procédures, on peut presque deviner ce que fait le programme. Plus généralement, lorsqu’une séquence se retrouve plusieurs fois dans un logiciel, il devient moins couteux de ne l’écrire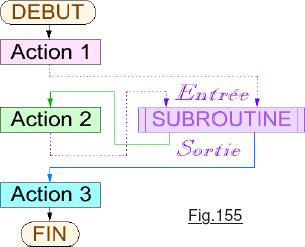 
qu’une seule fois sous forme d’une subroutine, et de l’invoquer chaque fois qu’il y en a besoin. Cette façon d’organiser un logiciel est naturelle, toutefois elle engendre un problème technique épineux. En effet, dans la séquence de la Fig.154 chaque bloc sait où se trouve la suite du programme, car une seule transition de « branchement » est utilisée. Il en va tout autrement sur la Fig.155 où l’on fait appel deux fois à la subroutine, avec chaque fois une « adresse de retour » différente. C’est précisément dans la gestion des adresses de retour dans le programme appelant que réside la difficulté. Sans entrer dans les détails, sur les processeurs actuels un dispositif logique interne est dédié à la gestion des appels et retours de procédures, ainsi que celle des variables dites locales. Chaque fois que le programme « principal » fait appel à une procédure, il emPILE l’adresse de retour. Plusieurs procédures peuvent être invoquées. Dès que l’une d’elle trouve l’instruction de retour, le mécanisme logique déPILE la dernière adresse enregistrée. C’est ainsi que sont gérés de façon « très simple » les appels à fonction ou procédures, qu’elles soient invoquées une seule fois ou un nombre quelconque. Il se trouve que par principe une Machine de Turing n’est pas pourvue d’une telle organisation logique. (PILE et « stack pointeur ».) Nous somme donc naturellement incités à nous demander si intégrer l’utilisation d’une procédure invoquée plusieurs fois est possible en respectant scrupuleusement le concept de l’illustre mathématicien.
Un défi à relever.
Pratiquement tous les mathématicien avec pour complices les informaticiens s’accordent à considérer que tout ce que peut faire un ordinateur actuel quelle que soit sa puissance, une machine de Turing existe et en est capable. La réciproque n’est pas forcément vraie. Bien entendu il n’est absolument pas question ici de le prouver ! En revanche, si nous arrivons à coder une organisation logicielle telle que celle de la Fig.155, non seulement on aura ouvert une piste de recherche très intéressante, et surtout on aura fait pencher la balance du bon coté, sans pour autant que ce soit une démonstration. Dans ce chapitre je vous invite à relever le défi. Pour que l’exercice soit démonstratif, on va utiliser la machine la plus puissante mise à notre disposition, c’est à dire que l’on va activer le mode ÉTENDU pour disposer de 20 transitions dans la matrice virtuelle. Je vous propose les contraintes suivantes :
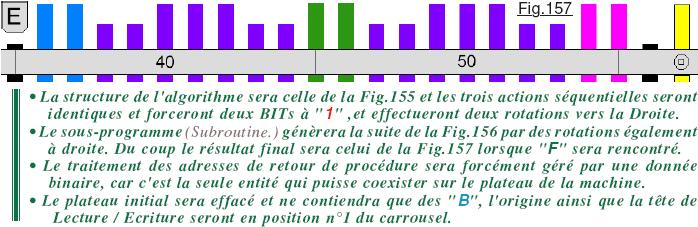
Une solution possible pour relever ce défi est proposée dans le tableau ci-dssous. Ce dernier est paginé sens dessus dessous pour vous éviter de voir cet algorithme sans le vouloir, ainsi le charme de vous « cogner » à cet algorithme et d’en découvrir la subtilité est préservé. Il faut penser « Turing », c’est à dire traiter le comportement du programme et de la PILE comme une donnée binaire ordinaire.
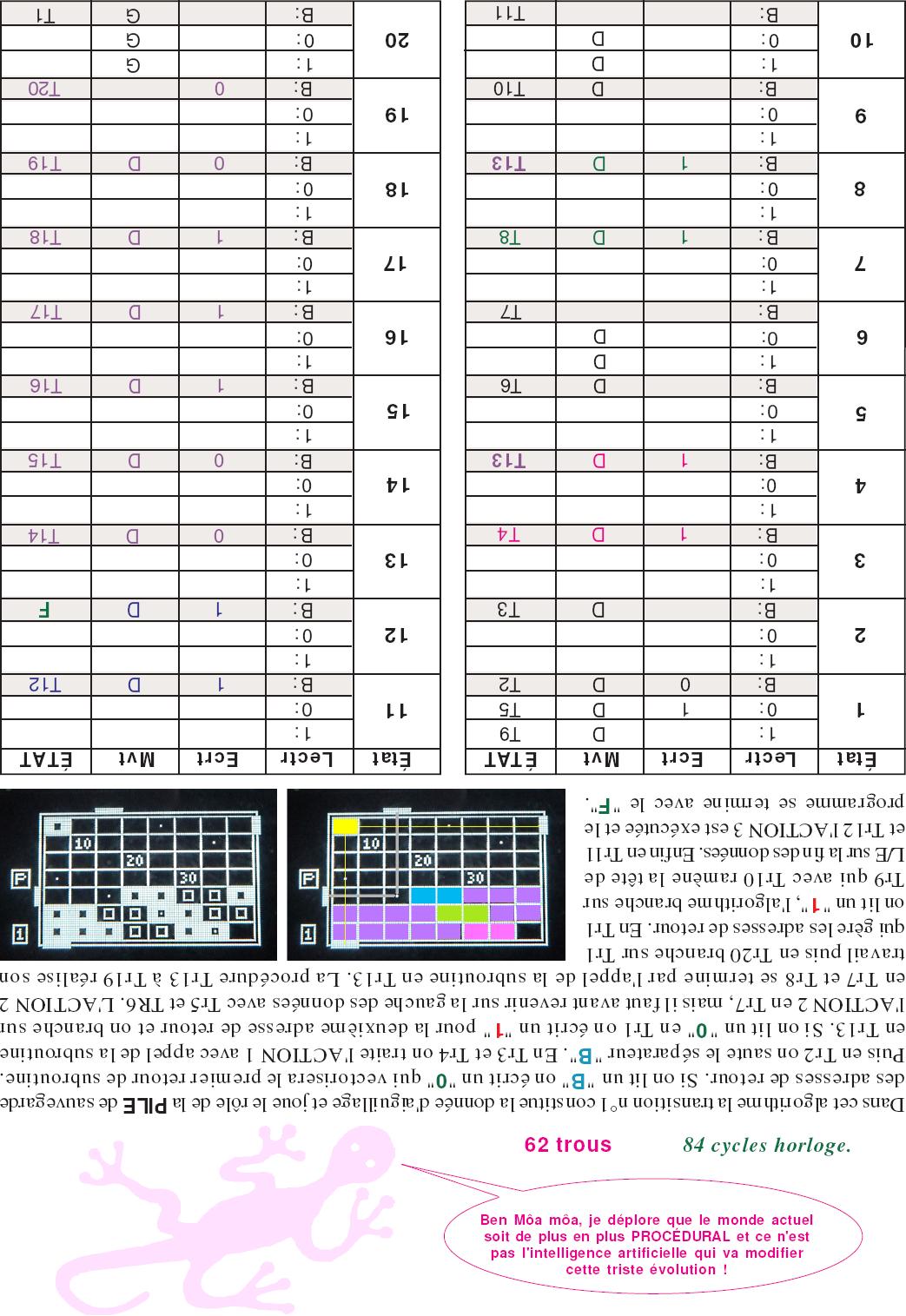
La fin est ici
