Bonjour,
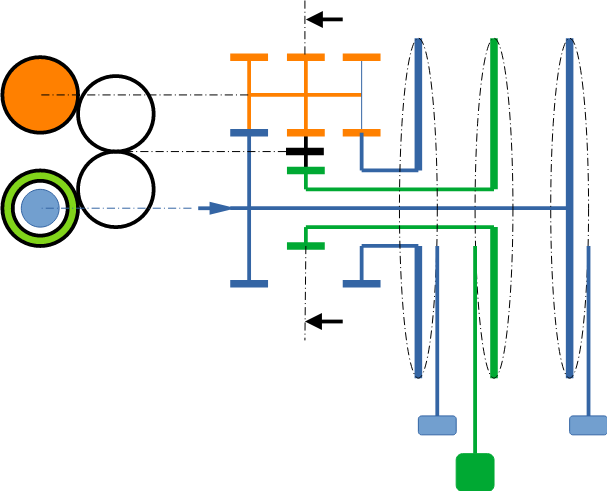
Je dois calculer la somme des puissances sur l’axe d’entrée de l’assemblage mécanique que voici :
Les trois treuils (2bleus et 1 vert) ont le même diamètre.
L’axe d’entrée (bleu) tourne à ω ainsi que les 2 treuils bleus. Grâce au réducteur non inverseur de rapport 0,5, le treuil vert tourne à 2ω.
Un poids x est relier au treuil vert, de sorte que son poids s’oppose à la motricité.
2 poids y = x/2 sont reliés chacun aux treuils bleus du même coté, mais du coté opposé au poids du treuil vert. De sorte que leur poids soient en addition à la motricité.
La puissance motrice est égale à Pm
La puissance pour déplacer chaque poids y est égale à Py
La puissance pour déplacer le poids x est égale à Px
Sans considération des pertes mécaniques la somme des puissances (Ps) pour déplacer les poids est Ps = Px + 2Py
Sans considération des pertes, les engrenages transmettent toujours l’intégralité des puissances qu’ils reçoivent.
Calculs :
Le poids x s’oppose à la motricité je dois lui donner le signe moins(-).
Couple du poids x, -Cx = -Fx*R
-Px = -Cx*2ω
Couple d’un poids y, Cy = Fy*R = (|Fx|/2)*R
Sans signe pour |Fx|, je pense que l’on dit en valeur absolue.
Py = [(|Fx|/2)*R]*ω
Première hypothèse :
Les poids y sont en addition à la motricité je peux les additionner.
2Py = [(|Fx|/2*R)*ω]*2 = (|Fx|*R)*2ω = |Px|
Ou 2Py = [(Fy*R)*ω]*2 = (2Fy*R)*2ω = |Px|
Sommes des puissances pour déplacer les poids Ps = 2Py - Px = 0
Les poids sont équilibrés et la motricité n’assume que les pertes mécaniques.
Deuxième hypothèse :
2Py = [(|Fx|/2*R)*ω]*2 = |Fx|*R*ω = (|Px|/2)
Ou 2Py = [(Fy*R)*ω]*2 = Fy*R*ω*2 = (|Px|/2)
Somme des puissances pour déplacer les poids Ps = 2Py- Px = -Px/2
Les poids ne sont pas équilibrés et la motricité doit assumer -Px/2.
Quelle est la bonne hypothèse ?