10 réponses à ce sujet

[Zénon]

Bonjour,

 

J'ai précédemment posté des sujets avec des liens. Hélas parfois les hébergements sont provisoires, car gratuit. Je vais donc éviter cette pratique à l'avenir.

Je vous propose un système d'engrenages qui parait sans intérêt. Je vous parlerais par la suite des applications que j'envisage.

Avant toute chose je souhaiterais savoir si le fonctionnement que j'imagine est correcte.

_ Si un couple Co est appliqué sur l’axe orange, il est peu probable, que l’axe mauve tourne.

Car l’appui du pignon 2 sur la carcasse bloquerait Co, par une tentative de déplacement antagonistes du porte-satellites vert, par rapport au pignon 1. Toutefois le couple (Co) resterait effectif sur l’axe mauve.

_ L’axe mauve peut-être menant dans les deux sens si un couple Cm lui est appliqué.

Néanmoins, Cm doit être éventuellement supérieur à Co et aux pertes mécaniques, pour faire tourner les deux satellites 1 et 2 avec le porte-satellites vert.

Le porte-satellite vert tournerait alors dans le sens du couple Cm. Le pignon satellite 1, suivrait le même mouvement que le pignon satellite 2, sans influencer la couronne bleue. Car sa rotation et son déplacement (révolution) lui sont imposé par le planétaire mauve et le porte-satellites vert.

De ce fait la couronne bleue resterait immobile, que Co soit ou non effectif sur l’axe orange.

L’opposition de Co et Cm se réaliserait sur le prote-satellites vert.

Merci de bien vouloir me répondre.

 

 

[Mike118]

j'ai l'impression que tu essayes de mettre plusieurs trains épicycloïdaux en série. 

Est ce que tu connais les formules qui lient les vitesses de rotations des planétaires  (P1 et P2), satellites (S) et porte satellite (PS ) d'un train épicycloïdal?   

Il faut découper ton montage en plusieurs parties : 

Partie 1 : 


Orange est un planétaire P1, c'est ton entrée 
Le bâti en noir c'est le porte satellite PS qui est fixe. 
En rouge c'est le satellite S, 
en Bleu c'est le deuxième planétaire P2 qui est ta sortie. 


On est capable d'exprimer la vitesse de bleu et le couple reçu en fonction de la vitesse d'orange P1 et du couple d'orange P1 et du nombre de dents sur P1 P2 S et PS... 

De la forme : 

•  Wbleu = K1 Worange   (1)

Une fois que tu as la vitesse de P2, tu peux continuer ton analyse 

On peux identifier un autre train épi : 


Dans ce cas tu peux exprimer la vitesse du PS vert en fonction de la vitesse du Planétaire P1 violet,  ( tu as S qui est en rouge et P2 qui est le bâti fixe en noir )  et tu vas avoir un résultat de la forme suivante :

 

• Wvert = K2 W violet  (2)

Enfin tu as un 3 ème train : 


Celui ci n'a rien de fixé , donc tu peux uniquement exprimer la vitesse de Bleu en fonction de vert et violet, ...  avec un résultat de la forme 

• W bleu = K3 Wvert + K4 W violet  (3) 

Ce qui te donne  en réutilisant (2)

W bleu = K3 * K2 W violet + K4 W Violet       =>    W bleu =   (K3 * K2 + K4) W violet 

Ce qui en reprenant la formule (1)  trouvée avec le premier train épi nous donne : 

K1 W orange  = (K3 * K2 + K4) W violet  

Et donc on a une relation directe entre la vitesse d'orange et de violet ... 

W violet =   W orange * K1 /   (K3 * K2 + K4) 


Je t'invite à creuser les formules des trains épicycloïdaux pour retrouver les valeurs de K1 K2 K3 et K4 en fonctions des dents des engrenages en jeux. 
 

[Zénon]

Bonjour,

Merci MIKE118, je vais réfléchir sur tes explications, je pense pouvoir les comprendre.

C'est toujours bien d'avoir une ou plusieurs pistes de réflexion.

Ainsi je pourrais savoir si un couple sur l'axe orange s'auto-bloque ou non et si un couple sur l'axe mauve peut faire tourner l'axe mauve en laissant la couronne bleue immobile.

Je pourrais peut-être aussi savoir si le couple sur l'axe mauve doit vaincre le couple sur l'axe orange quand il y en a un.

Du moins j'espère pouvoir répondre à ces interrogations.

[Zénon]

Bonjour,

 

Encore merci MIKE118, tes recommandations mon permis d’y voir plus clair.

Bien que mes cours datent de 55 ans, à l’époque nous ne parlions pas de tenseur, j’ai fait de mon mieux pour vous donner le maximum d’informations.

Si je ne me trompe pas, j’ai la réponse à mes interrogations en résumé. Voici comment je comprends le fonctionnement :

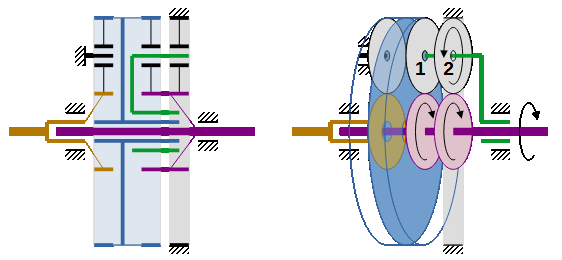
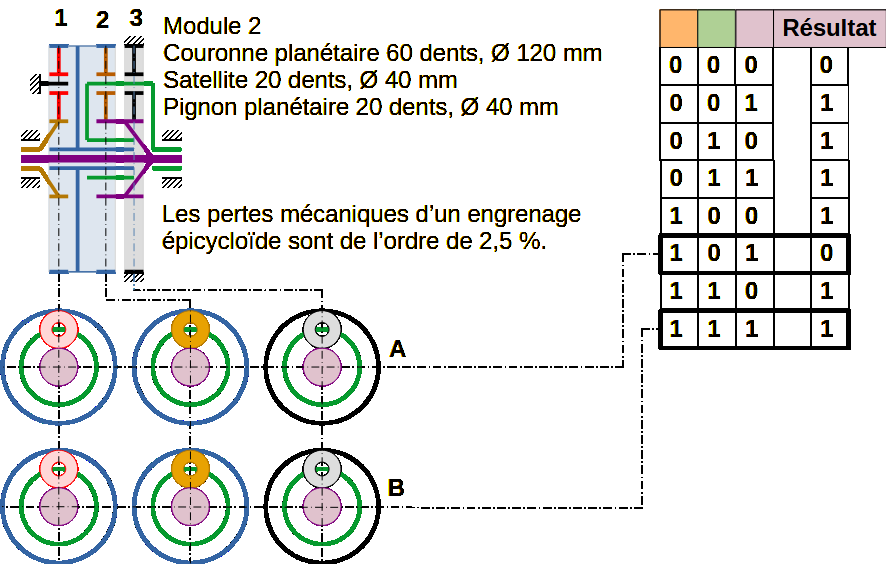
Caractéristiques : Module 2, Unité 1 N/m/s = 1 W

_ Couronne planétaire 60 dents, Ø 120 mm

_ Satellites 20 dents, Ø 40 mm

_ Pignon planétaire 20 dents, Ø 40 mm

_ Couple menant = 10 N/m

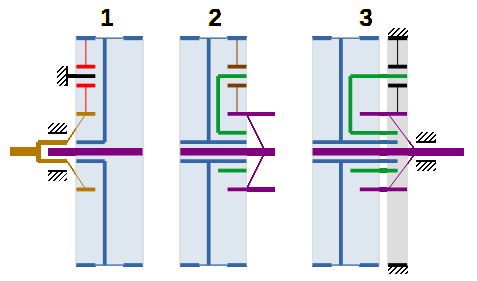
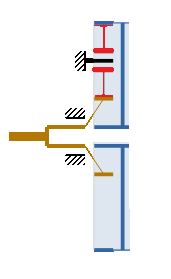
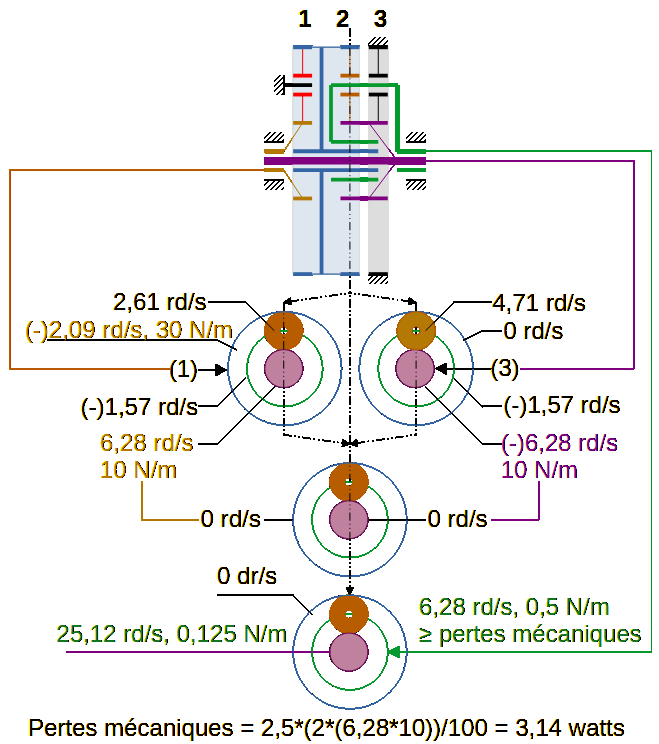
Élément menant en (1) : Planétaire orange ω =200 rd/s à 10 N/m

Couple résultant sur le planétaire bleu = -30 N/m à -66,6666666 rd/s

W planétaire bleu = |(-30*-66,67)| = W planétaire orange = |(10*200)|

Le couple résultant sur le planétaire mauve (2) devrait-être de (+10 N/m à 200 rd/s) à condition que les engrenages puissent tourner, ce qui n’est pas le cas. Car les vitesses de rotation des satellites noir et marron seraient différentes. C’est incompatible, il y a un auto-blocage, les engrenages resteront fixes. Cependant le couple résultant sur le planétaire mauve reste effectif d’une valeur de (+10 N/m).

 

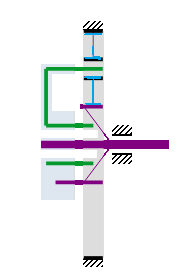
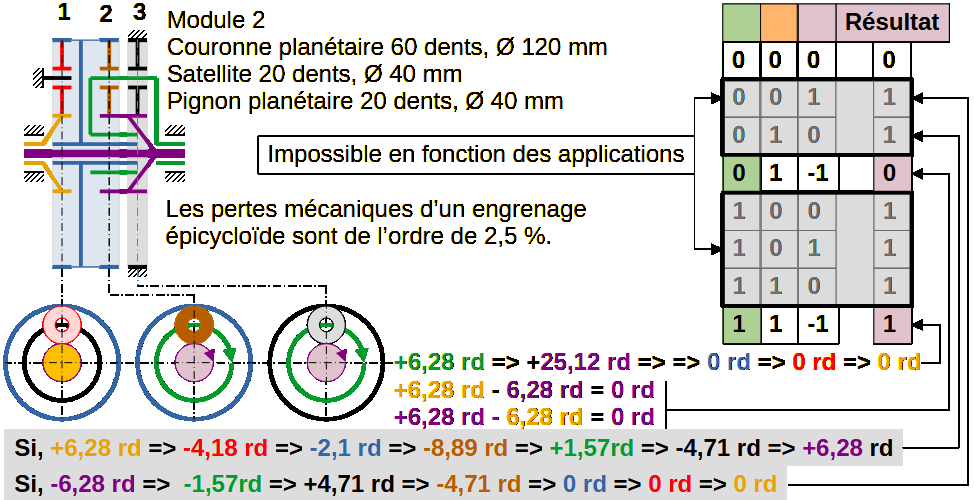
Élément menant en (3) : Planétaire mauve ω = -200 rd/s, (-10 N/m) => (-) car inverse de ω.

Couple résultant sur le porte-satellites vert = -40 N/m à -50 rd/s

Le satellite marron (2) est libre sur le porte-satellites vert, se qui donne un couple nul sur le planétaire bleu. Le satellite marron tourne à la vitesse angulaire du satellite noir et le planétaire mauve est incapable de transmettre un couple sur le planétaire bleu.

Car => W résultante sur le planétaire bleu = (-10*-200) - (-40*-50) = 0 W => 0 N/m

W porte-satellites vert = |(-50*-40)| = W planétaire mauve = |(-10*-200)|

 

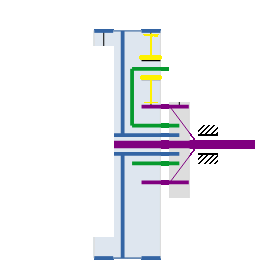
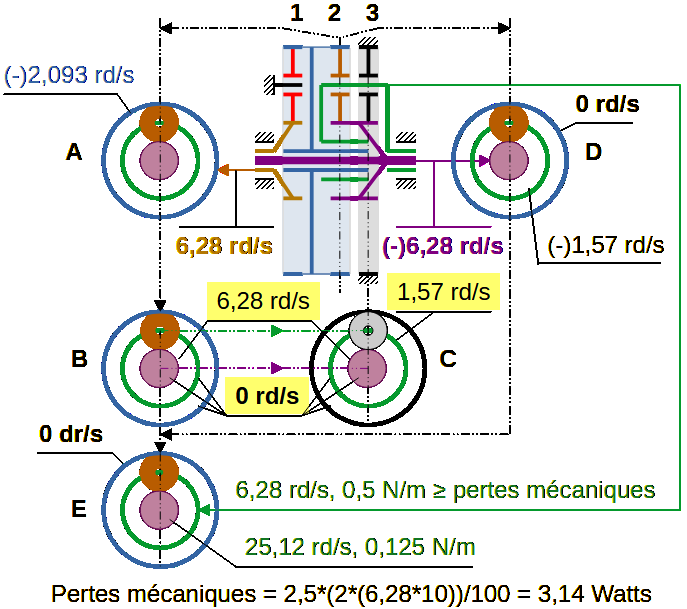
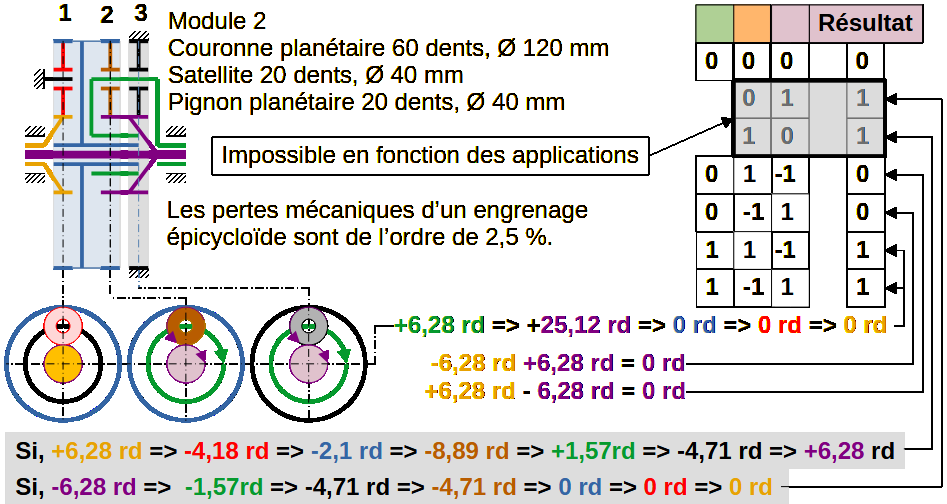
Éléments menants : Planétaire orange (+10 N/m) et planétaire mauve (-10 N/m)

Le satellite marron reçoit diamétralement deux couples égaux et de même signe mathématique, du planétaire bleu (-10 N/m) et du planétaire mauve (-10 N/m).

Couple résultant sur le porte-satellite vert = (-20 N/m). Ce couple est incapable de mettre en mouvement les engrenages, car il est issu de l’équilibre entre les couples (-10 N/m) et (-10 N/m).

Le couple (-10 N/m) bloque les engrenages, le couple opposé (-10 N/m) ne fait qu’équilibrer le couple (-10 N/m), Ce qui laisse les engrenages immobiles en position d’équilibre.

Pour faire tourner le planétaire mauve, il faut un couple supérieur à (-10 N/m) ou bien apporter au porte-satellites vert un couple qui déséquilibre les couples des planétaires orange et mauve.

 

En résumé :

Deux couples égaux et opposés sur les axes orange et mauve s’équilibrent et sont incapables de mettre les engrenages en rotation.

Toutefois, un troisième couple sur le porte satellites vert, supérieur aux pertes mécaniques est capable de mettre en mouvement les engrenages et l’axe mauve. L’axe orange reste immobile bien qu’il soit soumis à un couple opposé et égal à celui de l’axe mauve.

[Zénon]

Bonjour,

 

Je pense m'être planté et je sais où.

Je recommence.

A+

[Zénon]

Bonjour,

Si je ne me suis pas trompé, voilà une étude plus complète.

Caractéristiques : Module 2.  Conversion 1 N/m/s = 1 Watt

_ Le couple de 0,5 N/m sur le porte-satellites vert, donne la référence de rotation (+)

_ Couronne planétaire 60 dents, Ø 120 mm

_ Satellites 20 dents, Ø 40 mm

_ Pignon planétaire 20 dents, Ø 40 mm

_ Couple menant sur l’axe orange = 10N/m à 6,28 rd/s

_ Épicycloïde (1) rapport de multiplication 1/3

_ Couple menant sur l’axe mauve = 10 N/m à (-)6,28 rd/s

_ Épicycloïde (3) rapport de multiplication 1/4

_ L’étude est réalisée pour un tour (6,28 rd) des axes, orange, mauve et du porte-satellites vert.

_ Les pertes mécaniques dans un engrenage épicycloïde sont de l’ordre de 2,5 %

> Les couples égaux et opposés sur les planétaires oranges et mauve, laissent les engrenages en équilibre immobile. Cependant ces couples, restent effectifs.

> Toutefois, un troisième couple supérieur aux pertes mécaniques sur le porte-satellites vert, met en rotation les engrenages des épicycloïdes (2) et (3), en laissant le planétaire bleu et orange immobile.

 

[Zénon]

Bonjour,

Je suis surpris par l'absence de commentaire.

Je me suis peut-être mal expliqué ?

Je vous ai donc fait un schéma avec une explication qui j'espère est plus précise et plus compréhensible.

 

Caractéristiques : Module 2 Conversion : 1 N/m/s = 1 Watt 360° = 6,28 rd

_ Le couple de 0,5 N/m sur le porte-satellites vert, donne la référence de rotation (+)

_ Couronne planétaire 60 dents, Ø 120 mm

_ Satellites 20 dents, Ø 40 mm

_ Pignon planétaire 20 dents, Ø 40 mm

_ Couple menant sur l’axe orange = 10N/m à 6,28 rd/s

_ Épicycloïde (1) rapport de multiplication 1/3

_ Couple menant sur l’axe mauve = 10 N/m à -6,28 rd/s

_ Épicycloïde (3) rapport de multiplication 1/4

_ Épicycloïde (2) tous les pignons sont libres.

_ L’étude concerne un tour des axes orange et mauve, puis un tour du porte-satellites vert.

_ Les pertes mécaniques dans un engrenage épicycloïde sont de l’ordre de 2,5 %

_ Important : dans les applications prévues, les planétaires orange et mauve reçoivent des couples égaux et opposés avec un différentiel de rotation (≠ω) commun, donc (+ω) et (-ω). Cette condition est imposée par les applications.

Les rapports de multiplication (1/3 et 1/4) entre les épicycloïdes (1) et (3), rendent la rotation des épicycloïdes (1), (2) et (3), impossible, avec le couple planétaire orange. Néanmoins le couple planétaire orange reste effectif sur le planétaire mauve.

De sorte que pour faire tourner le planétaires mauve en sens inverse du planétaire orange, il faut lui appliquer un couple opposé supérieur à celui du planétaire orange. Si les couples sont égaux et opposés, les engrenages libres, resteront immobiles en équilibre. Toutefois, un troisième couple supérieur aux pertes mécaniques sur le porte-satellites vert, met en rotation les engrenages des épicycloïdes (2) et (3), en laissant le planétaire bleu et orange immobile. Les couples égaux et opposés en équilibre des planétaires orange et mauve sont alors incapables d’influencer le couple sur le porte-satellites vert.

[Zénon]

Bonjour,

Je ne sais que penser de l'absence de réponses.

En attendant, je vous présente une explication supplémentaire.

 

Application au levage des charges:

Si une charge est suspendue au treuil.

_ Le câble est fixé au disque orange et au treuil, de façon diamétralement opposée et divisent le poids de la charge par deux.

_ Les deux couples égaux et opposés, sont équilibrés.

_ l’axe vert peut entraîner l’axe mauve, sans s’opposer à la gravité et lève la charge en n’assumant que les pertes mécanique ; similaire aux systèmes à contrepoids, sans la contrainte du contrepoids.

Rien ne se perd, rien ne se crée sur l’épicycloïde 2

_ Sans l’épicycloïde (3), le planétaire bleu fournirait (car un travail/s), -62,8 N/m/s. Il tournerait à -2,09 rd/s, plus vite que le porte-satellites (PS) vert à -1,57 rd/s.

_ Cette différence de rotation maintient l’opposition du planétaire bleu sur le mauve.

_ Dans tous les cas concernés : Le planétaire mauve développe -62,8 N/m/s.

Sa rotation déplace le point A en B à -1,57 rd/s.

_ Le satellite marron reçoit les puissances opposées des planétaires bleu et mauve, (-62,8 N/m/s) et maintient le planétaire bleu immobile.

 

Il faut (-62,8/4) = -15,7 N/m/s, sur le satellite marron, pour immobiliser le planétaire bleu pendant le déplacement du point A en B.

Cette puissance est fournie par le planétaire mauve : (-62,8/4) = -15,7 N/m/s.

Σ des puissances appliquées au satellite marron : (-15,7) - (-15,7) = 0 => Équilibre des engrenages.

 

La charge reste donc immobile, suspendue au treuil sans un apport de puissance sur le PS vert.

 

 

[Zénon]

Bonjour,

J'ai trouvé une méthode plus simple pour expliquer le fonctionnement du train d'engrenages et je retrouve toujours le même résultat.

J'espère ainsi avoir un message en réaction ou aurais-je aussi réussit à équilibrer cette forme de réaction. (Je plaisante)

 

Le couple orange est immobilisé dans les engrenages. Car la tentative de rotation à -4,18 rd/s du satellite marron plus ((+) car les signes sont identiques) la rotation à -2,1 rd/s du planétaire bleu nécessitent un PS vert immobile, pour faire tourner le planétaire mauve à +6,28 rd/s (car c’est un épicycloïde inverseur). Or, si le planétaire mauve tourne il est impératif que le PS vert se déplace, car le satellite noir est en appuis sur le planétaire fixe de carcasse. Le couple orange reste donc effectif, en appuis sur le planétaire mauve sans mettre les engrenages en mouvement.

 

Le couple mauve entraînerait le planétaire mauve à -6,28 rd/s, laissant le planétaire bleu immobile. Car la rotation du PS vert à -1,57 rd/s, moins ((-) car les signes sont contraires) la rotation du satellite marron à +4,71 rd/s, donne -6,28 rd/s du planétaire mauve (-1,57 - (+4,71)) = -6,28 rd/s.

Cependant, le planétaire bleu toujours en appuis sur le planétaire mauve tente de le faire tourner à +6,28 rd/s. Sans considération des pertes mécaniques, les engrenages transmettent toujours la puissance qu’il reçoivent. De ce fait, les couples étant égaux et opposés, leur soustraction (car ils sont opposés) donne un résultat : Σ = (6,28*10) - (-6,28*-10) = 0 => Le couple mauve laisse donc les engrenages immobiles en équilibre.

 

De ce fait, le couple vert supérieur aux pertes mécaniques sur le PS vert, met en rotation les engrenages des épicycloïdes (2) et (3), en laissant le planétaire bleu et orange immobile. Les couples égaux et opposés en équilibre des planétaires orange et mauve sont alors incapables d’influencer le couple vert. Similaire aux systèmes à contrepoids mais sans contrepoids.

 

Similitude :

Le poids orange est bloqué, cependant le poids mauve égal et opposé ne peut mettre en mouvement le système en équilibre.

Les différences et les avantages des engrenages sont :

_ Un blocage du poids orange à 360°.

_ Une rotation possible dans les deux sens (+ω ou -ω) du planétaire mauve.

_ Un auto-équilibrage de la réaction de charge.

 

[Zénon]

Bonjour,

Voici je pense la bonne analyse.

_ Important : dans les applications prévues, les planétaires orange et mauve reçoivent toujours des couples égaux et opposés avec un différentiel de rotation (≠ω) commun. Cette condition est imposée par les applications qui suivront. Les cas effectifs considérés sont donc A et B.

L’étude porte sur un tour ou 6,28 rd/s

 

Si, +6,28 rd orange => -4.18 rd rouge_ -2,1 rd bleu _ -8,89 rd marron _ +6,28 rd mauve _ +1,57rd vert  _ -4,71 rd noir

Si, -6,28 rd mauve => -1,57rd vert _ +4,71 rd noir _ -4,71 rd marron _ 0 rd bleu _ 0 rd rouge _ 0 rd orange

 

Cas A : Si des couples égaux et opposés sont appliqués sur les axes orange et mauve, les engrenages resterons immobiles en équilibre. => 0 rd orange et 0 rd mauve

 

Cas B : Un couple supérieur aux pertes mécaniques sur le PS vert, met en rotation les engrenages des épicycloïdes (2) et (3), en laissant le planétaire bleu et orange immobile. Les couples égaux et opposés en équilibre des planétaires orange et mauve sont alors incapables d’influencer le couple vert. Similaire aux systèmes à contrepoids mais sans contrepoids. => 6,28 rd vert _ 25,12 rd mauve

[Zénon]

Bonjour,

Je vous présente mes excuses pour les erreurs que j'ai fait dans le schéma précédant.

Voici la correction qui résume l'ensemble du fonctionnement.