83 réponses à ce sujet

[Mike118]

Bonjour,

Bon la j'ai a nouveau des soucis .
quand j'alume le robot la tension présente sur l'entré analogique de l'arduino pour la mesure de la tension pose problème en effet cela bloque le boot de l'arduino si le modul Xbee est présent.
la solution temporaire que j'utilise est de brancher l'entrée analogique apres le boot de l'arduino mais c'est pas tres commode.

quelqu'un a une idée pour regler ce problème ?

sinon j'installerais un intérupteur suplémentaire

merci d'avance.

Ajoute un condensateur il fera office de temporisateur et permettra à ta arduino de se boot avant que la tension sur l'entrée analogique soit trop importante pour l'empêche de booter. Bien choisir ce condensateur pour qu'il évite d'intérférer avec la fonction principale du reste du montage qui est la lecture de la tension !

J'espère que cette idée t'aidera !

[inovasong]

Ajoute un condensateur il fera office de temporisateur et permettra à ta arduino de se boot avant que la tension sur l'entrée analogique soit trop importante pour l'empêche de booter. Bien choisir ce condensateur pour qu'il évite d'intérférer avec la fonction principale du reste du montage qui est la lecture de la tension !

J'espère que cette idée t'aidera !

Ok je vais me pencher sur cette solution.
chouette encore un composant a aprofondire

[inovasong]

Bonjour,


Bon j'ai jeté un coup d'oeil sur deux ou trois documentions sur le sujet du condensateur, si j'ai bien compris le condensateur a un temps de charge et de décharge et il permet de lisser la tension . Le qui est un peux plus compliqué pour moi c'est comment choisir mon condensateur, donc un condensateur qui supporte la tension max appliqué a ces bornes donc dans mon cas 5v max , la ou j'ai du mal c'est a comprendre comment trouver un condensateur qui pourras ce charger en min 500ms sans perturber la mesure de la tension ?

au secours Help

[Black Templar]

Bonjour,


Bon j'ai jeté un coup d'oeil sur deux ou trois documentions sur le sujet du condensateur, si j'ai bien compris le condensateur a un temps de charge et de décharge et il permet de lisser la tension . Le qui est un peux plus compliqué pour moi c'est comment choisir mon condensateur, donc un condensateur qui supporte la tension max appliqué a ces bornes donc dans mon cas 5v max , la ou j'ai du mal c'est a comprendre comment trouver un condensateur qui pourras ce charger en min 500ms sans perturber la mesure de la tension ?

au secours Help

Le temps de charge est déterminé à la fois par la capacité du condensateur ainsi que par le courant entrant dans le condensateur. (i = C.dUc/dt)

Donc pour déterminer le temps de charge, il te fait à la fois une résistance et une capa
Le produit RC correspond à une constante de temps appelé Tau.
Au bout de Tau secondes, le condensateur s'est chargé à 63%, à 3.Tau, la capa est chargé à 95% et à 5.Tau, à 99%.
(C'est pareil pour la décharge)

L'équation de la tension aux bornes de la capa en fonction du temps est

• Pour la charge : Uc =Ualim . (1 - exp(-t/Tau))
• Pour la décharge : Uc = U0 . exp(-t/Rau)

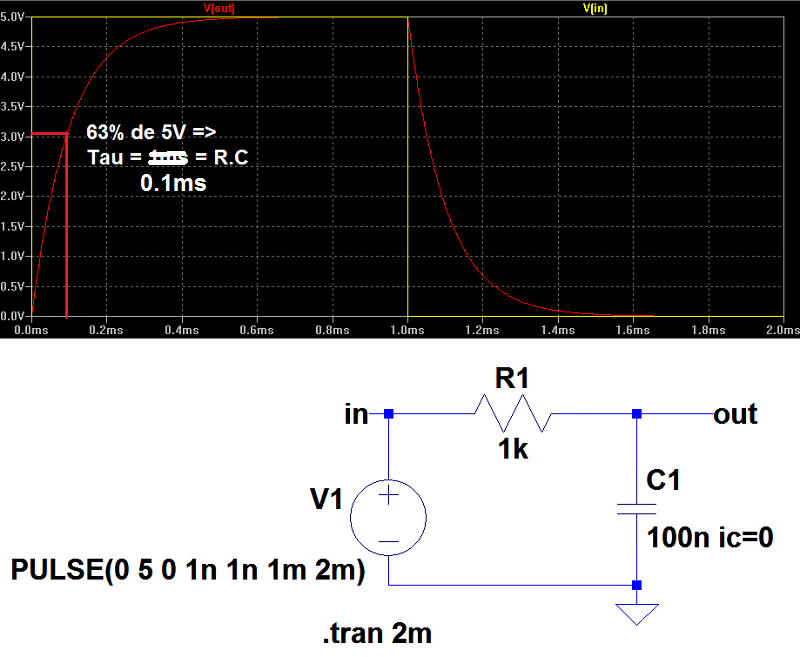
Petite simulation pour bien comprendre, R = 1 kohm, C = 100 nF
Tau = R.C = 1000 * 100 * 10^-9 = 0.0001 = 0.1ms





Enfin la partie plus mathématique qui permet de retrouver l'équation de la charge et de la décharge de la capa.
Dans le circuit, tu as un générateur, une résistance et une capa.
La loi fondamentale à connaitre pour la résistance est la loi d'ohm : Ur = R.ir
La loi fondamentale à connaitre pour la capa, c'est ic = C.dUc/dt (dUc/dt correspond à la dérivé dans le temps de la tension aux bornes de la capa)

On a donc l'intensité qui vaut C.dUc/dt, mais qui vaut aussi Ur/R car on est dans un circuit série.
On applique la loi des mailles : V1 = Uc + Ur, on isole Ur : Ur = V1 - Uc
On remplace Ur dans l'égalité précédente : C.dUc/dt = (V1-Uv)/R
On développe un peu et on obtient : RC.dUc/dt + Uc = V1

On a donc une équation différentielle qu'il suffit de résoudre pour retomber pil poil sur l'équation de la charge de la capa