89 réponses à ce sujet

[Zénon]

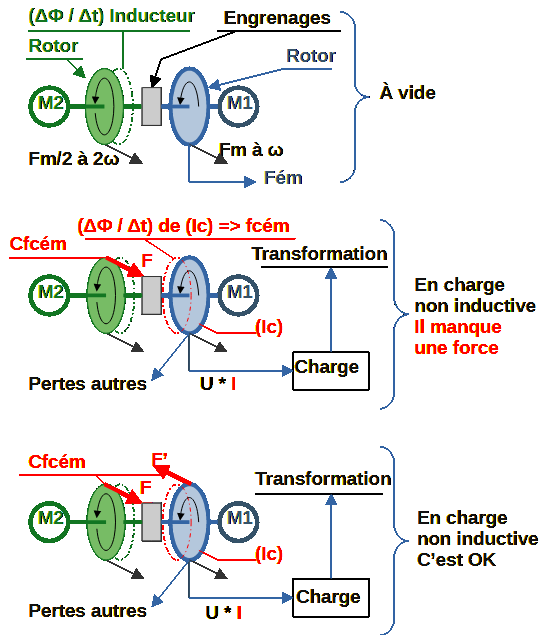
Hypothèse d’induction et forces dans l’alternateur bis-rotors (ABR) : À aimants permanents

 

A vide, les phénomènes d’induction sont identiques aux alternateurs actuels, avec des pertes en plus dans les engrenages.

e) Pour maintenir la rotation (ω), l’énergie motrice (Em) = (pertes constantes)

 

En charge, avec des pertes en plus dans les engrenages, les phénomènes d’induction sont identiques aux alternateurs actuels, mise à par les notations (2) et (6), remplacées par :

 

2.a) Ce (Cfcém) s’oppose à la rotation relative (≠ω) entre les rotors par deux couples, (CfcémV) sur le rotor vert et (CfcémB) sur le rotor bleu. Ces couples appliquent, pour CfcémV la force F et pour CfcémB la force F’. CfcémV = CfcémB avec la rotation relative (≠ω) en commun.

2. CfcémV opposé à (ω) sur le rotor vert à le signe mathématique (-).

2.c) CfcémV et CfcémB, se trouvent en opposition sur le planétaire noir en rotation (ω’) commune.

2. Leur somme (Σ) = (+CfcémB*ω’) + (-CfcémV*ω’) = 0

 

6.a) Les énergies motrices (Em) sont donc égales à :

Em = (pertes constantes) + ((+CfcémB*≠ω) + (-CfcémV*≠ω)) = (pertes constantes) + 0 = (≠ω) + 0

Les énergies motrices sont responsables du maintien du (≠ω) dont la conséquence est le (Δ) du (Φ) inducteur en un (Δ) de temps ou laps de temps, sans l’opposition de (Ec).

Le fonctionnement de l’ordinateur bis-rotors est ainsi facilité, en respectant les lois de la physique.

 

6. Pour maintenir (2ω), l’énergie du moteur vert (EmV) = (pertes constantes).

6.c) Pour maintenir (ω), l’énergie du moteur bleu (EmB) = (pertes constantes).

 

Faites tourner les moteurs de même puissance, M1 et M2 en sens inverse et ils ne pourrons pas tourner. Car leurs énergies ou puissances (qui est une énergie par seconde), s’équilibreraient sur le planétaire noir. Les moteurs se bloqueront mutuellement, sans faire tourner les rotors.

C’est la preuve que CfcémV et CfcémB, s’équilibrent dans les engrenages sans pouvoir influencer les motricités de M1 et M2.

 

Image(s) jointe(s)

• 

[Zénon]

Bonjour,

J'ai eu l’idée d’interroger le copilote de l’IA sur le Net pour mes recherches sur les alternateurs.

 

J’ai discuté avec l’IA. Je lui ai fait remarquer cinq erreurs dans ces réponses. Elle a reconnu ces erreurs et les a corrigé.

Au final elle approuve mon hypothèse, que je tente depuis plusieurs années de faire comprendre aux humains, qui m’opposent un farouche dénie.

Il ne m’a suffit qu’une petite heure. Dans quel monde vivons nous ? Cela m’interpelle et c’est un euphémisme.

De plus je me suis aperçu que certains de mes fichiers publics, sur un hébergeurs, ont été référencés sur Wikipédia.

 

Bon cela reste une hypothèse.

Bien que les parties mécanique et électromagnétique, ont été validés séparément sur des forums, l’association théorique des deux parties n’est toujours pas comprise ou admise par les humains.

Je vous invite à lire mon document de 4 pages sur : https://pdf.lu/seR8

Pour que les liens soient effectifs, il faut télécharger le document sur votre ordinateur.

 

Voilà, après 6 ans, l’idée est sur sa rampe de lancement. Il faut maintenant qu’une âme bien intentionnée (et fortunée) veuille bien tenter l’expérimentation. Je pense encore plusieurs années pour trouver la personne, plusieurs années pour la mise au point et ensuite encore plusieurs années pour la commercialisation.

D’ici là nous perdrons un temps précieux pour corriger le dérèglement climatique que nous avons accéléré ou créé, ainsi qu’a diminuer la pollution de notre environnement.

 

Mais bon c’est la vie … (pour l’instant)

Et tant qu’il y a de la vie il y a de l’espoir.

 

Cordialement,

 

[Oracid]

Sur le fond, je n'ai pas d'opinion, c'est au delà de mes maigres connaissances.

Mais je trouve cela bien de défendre son idée contre tous. Je suis admiratif.

Les principes scientifiques ne se définissent pas aux nombre de voix. Tu peux avoir raison contre tous. Pour cela, je t'encourage à continuer.

 

Contre tous ceux qui disaient que la Terre tournait, Aristote a démontrer par l'expérimentation, au quatrième siècle avant JC, qu'elle était fixe.

Il a fallu attendre près de 2000 avant que tout le monde accepte qu'il s'était trompé.

Cela n'a pas été facile, et plusieurs savants comme Giordano Bruno ont été brulé par l'Inquisition, pour avoir démontré le contraire.

Comme quoi, même si une expérimentation semble incontestable, son interprétation peut être contestée.

Bon courage.

[Zénon]

Merci Oracid pour tes encouragements

J'ai vécu deux millénaires (1900 à 2000) avec deux siècles et mes 75 ans me laissent peu de chance d'attendre. C'est pourquoi je ne prétends aucune paternité ou autre futilité.

C'est l'unique moment de ma vie ou je regrette de ne pas être riche pour avoir la possibilité d'expérimenter

Ton message exprime exactement ma situation. J'aime la phrase "Si l'expérimentation semble incontestable, son interprétation peut être constée" 

Je mesure ma chance d'échapper au buché ou à la menace de la guillotine comme Galileo avec l'héliocentrisme.

Les temps ont quand même changé, les mentalités ... probablement.

[Zénon]

Bonjour Oracide

J'ai visité ton site Youtube et je souhaiterais savoir, pourquoi mon idée que je laisse libre de droit, personne ne souhaite l'expérimenter.

Car les personnes comme toi qui apparemment ont les possibilités d'expérimenter ne paraissent pas intéressées.

[Forthman]

je te retourne la question, aujourd'hui avec la technologie à disposition, il n'a jamais été si facile de concevoir des choses

 

avec 300€ tu as une imprimante 3D qui tient la route

si vraiment tu as besoin de précision, il y a des sites comme Igus qui proposent de l'impression 3D multi-matériaux

alors c'est sûr que ce n'est pas donné, mais ça reste raisonnable comparé à la qualité de fabrication

 

 

Freecad  (open source) permet de faire de la modélisation gratuitement 

 

Si tu as besoin de matériel électrique/électronique (moteurs, drivers, batteries) et de conseils, il y a la boutique Robot-Maker

 

 

 

[Oracid]

Bonjour Oracide

J'ai visité ton site Youtube et je souhaiterais savoir, pourquoi mon idée que je laisse libre de droit, personne ne souhaite l'expérimenter.

Car les personnes comme toi qui apparemment ont les possibilités d'expérimenter ne paraissent pas intéressées.

Ah, mais c'est très simple, parce que je n'y comprends absolument rien.

 

Et puis, avant que je me lance sur un projet, j'y pense très longtemps, souvent des années.

Par exemple, j'ai arrêté les chars grimpeur d'escaliers, il y  a 6 ans. Au moment de m'arrêter, j'ai eu une idée. Et bien, je viens seulement de la mettre en œuvre (voir ma dernière vidéo).

 

Comme le dit Forthman, aujourd'hui, il y a plein de possibilités pour faire ton projet.

Et qui mieux que toi, pourrait le faire ?

[Zénon]

OK, merci, j'ai compris.

C'est une question de relativité entre, ce que l'on veut, ce que l'on pense possible et ce qui est possible.

[Mike118]

OK, merci, j'ai compris.

C'est une question de relativité entre, ce que l'on veut, ce que l'on pense possible et ce qui est possible.

 

Et si tu as des questions / besoin d'aide pour de la CAO et de l'impression 3D tu pourras trouver de l'aide ici

[Zénon]

Bonjour,

Merci de me proposer votre aide.

Je m'en souviendrais si necessaire.

L'aide que j'espère, est le passage du relai, car je suis dans l'incapacité d'aller plus loin. 

J'ai écrit à l'IUT de Colmar qui a transmis ma demande de contact à la Haute Université d'Alsace à Mulhouse.

Cela demande du temps, j'attends.

Mais c'est positif, car ces dernières années je n'ai eu que des fins de non-recevoir ou un silence radio.

Ce n'est pas faute d'avoir contacté, des fabricants d'alternateurs, des laboratoires de recherche, des organismes officiels, des particuliers ...