22) La RÉCURSIVITÉ.

C’est manifestement l’Arlésienne dans le monde du logiciel. On en parle souvent, mais on ne la voit presque jamais. Vous proposer « une bible » du langage C++ sans aborder le chapitre de la récursivité serait un peu comme la Joconde sans ses lunettes : Il manquerait quelque chose de fondamental. (Oui, je sais que Mona Lisa au Louvre n’en porte pas, mais quand il y a du public elle les enlève par coquetterie !) Bon, après ce petit délire revenons à notre thème.

Les boucles itératives.

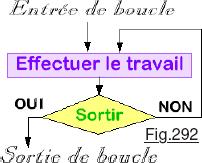
Risquant de « défoncer une porte ouverte », il me semble toutefois pertinent de bien présenter les boucles avant d’aborder sereinement la récursivité. Fondamentalement, il y a deux sortes de boucles. En fait il y a aussi les boucles dont on ne sort jamais. Dans ce cas c’est en général une erreur de programme, sauf pour le cas particulier de void loop(). Représenté sur la Fig.292 on a une boucle dans laquelle on commence par effectuer le travail. Puis on se demande si c’est terminé ou s’il faut recommencer. En C++ ce sont les boucle de type for, la condition de sortie étant exprimée dans les paramètres. Ce type de boucle est à privilégier lorsque l’action doit être réalisée au moins une fois. Par exemple un robot se trouve dans une pièce vers le centre. On désire qu’il se déplace jusqu’à toucher avec sa main un mur. Inutile de commencer à tester s’il y est arrivé, commençons par le faire avancer. Proposée sur la Fig.293 on a une boucle dans laquelle on commence par vérifier si l’on peut effectuer le travail avant de passer à l’action. En C++ ce sont les boucles de type while. Ce type de boucle est à choisir impérativement si l’action peut engendrer un risque. Par exemple nous ne savons pas où se trouve le robot. Le faire avancer peut le faire entrer en collision avec le mur s’il est déjà en contact avec ce dernier. (Ou par exemple comme effectuer une opération de division sans vérifier au préalable la nullité du diviseur etc.)

Les procédures récursives.

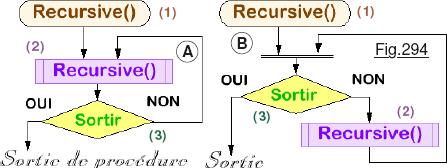Par nature, une procédure récursive est avant tout une boucle. Résumé sur la Fig.294, par définition une boucle est récursive lorsque dans son corps elle s’invoque au moins une fois. C’est un peu comme le serpent qui se mord la queue. Le fait qu’elle soit récursive impose comme pour toute boucle d’introduire un test pour détecter le moment d’en sortir. Comme pour les boucles itératives on peut effectuer l’action, puis le test de sortie montré en A ou l’inverse représenté en B. Dans les deux cas, on est en présence d’une procédure, c’est à dire une séquence d’instruction qui est invoquée par le programme. Lorsqu’elle a terminé son travail, le processeur revient à la suite de l’instruction d’appel. Dans les deux cas, lors de l’appel on « entre » de façon banale en (1) dans void dont ici le nom de l’identificateur est Recursive. En A on commence par le traitement spécifique en (2) … qui consiste à auto invoquer Recursive. Quand s’étant appelée un certain nombre de fois le travail est achevé, en (3) on revient au programme. Si pour effectuer le travail la procédure s’est invoquée 20 fois, alors en (3) elle va sortir 20 fois d’elle même ! Le cas B est analogue, sauf qu’en (3) on effectue 20 fois la vérification, puis c’est en « sortant 20 fois » d’elle même en (2) que le travail sera effectué. Il me semble évident que ces explications absconse vont vous laisser perplexes. Aussi, inutile d’ajouter encore plus de confusion, on va passer directement à la pratique et analyser ensemble le pourquoi du comment et les subtilités de la récursivité qui se montre aussi séduisante et mystérieuse qu’une sirène …

Experience_143 : Les bases de la récursivité.

Dans un premier temps les procédures récursives seront du type A, c’est à dire que l’on effectue 20 fois l’action, puis quand le travail est terminé on procède à la sortie. L’action à traiter est élémentaire, elle consiste à afficher vingt fois une même lettre. Pour pouvoir comparer les procédures itératives et les procédures récursives, en itératif on va traiter successivement A et B. Les procédures récursives Affiche _B() et Affiche _D() sont strictement identiques et de type A. En tête de listage sont précisés les coûts en octets de chaque procédure. On observe que la boucle for pour afficher le ‘A‘ et la boucle while pour afficher le ‘B‘ ont des tailles identiques de 40 octets. Pour effectuer un traitement strictement identique, la récursivité consomme 10 octets de plus. Par ailleurs, avec for ou while le compteur est en variable locale alors qu’en récursif il faut impérativement une variable globale à loger en mémoire dynamique.
REMARQUE : Comme l’appel aux quatre procédures ne doit se faire qu’une seule fois, dans cet exemple j’ai utilisé l’instruction goto pour enliser void loop() dans une boucle INFINIe.

Analyse du fonctionnement récursif.

Pour mieux cerner le fonctionnement de la procédure récursive il faut comparer avec l’organigramme de la Fig.294 en A.

En (1) c’est l’entrée dans la procédure suite à l’appel du programme principal. Le microcontrôleur effectue alors le traitement (2) de façon « banale ». En (3) le processeur teste si le travail est entièrement achevé. Si ce n’est pas le cas, il faut continuer le traitement. C’est là que la « magie » de la récursivité s’invite. En standard, pour tout appel à une procédure le microcontrôleur empile l’adresse ADR actuelle dans le programme pour y revenir en sortie de procédure. Sauf qu’ici, le compilateur détecte que l’on est dans le corps de la procédure, aussi il se contente de faire un « goto » sans sauvegarder l’adresse actuelle. C’est donc plus rapide. Lorsque le test (3) détecte la fin du traitement, le saut « goto » n’a pas lieu et l’on poursuit sur l’accolade ‘}‘ qui marque la fin de la procédure. Comme seule l’adresse ADR à été empilée, c’est elle qui provoque directement le retour au programme principal.

Experience_144 : Traitement récursif après la condition de sortie.

Presque frère jumeau du démonstrateur précédent, Experience_144.ino présente une structure strictement identique et effectue un traitement totalement analogue. La différence principale réside dans l’architecture des deux procédures récursives qui dans cette manipulation effectuent tout le travail en sortie lorsque la condition de fin est avérée. Ce programme est également un peu plus élégant à mon sens, car il n’utilise plus le goto.

Experience_145 : Procédure récursive avec passage de paramètres.

Qu’elle soit Récursive, une procédure reste une procédure, c’est à dire que l’on peut lui passer des paramètres et elle peut intégrer des variables locales si le traitement qu’elle effectue l’exige. C’est précisément ce que prouve Experience_145.ino qui reçoit comme paramètres deux nombres entiers. Pour proposer un exemple simple à analyser, la procédure se contente d’en effectuer le produit par la méthode brute qui consiste à ajouter Y fois le nombre X au Resultat. Toujours dans l’optique de rester simple pour démontrer la validité des variables locales, on se contente de créer N et M, de leur donner une valeur identique. On ajoute N à Resultat, on retranche M et ainsi on a effectué un traitement tout en restant mathématiquement neutre pour la multiplication.

Experience_146 : Chronométrage récursif et itératif pour comparaison.

Encore un traitement élémentaire qui consiste à faire un million de fois le même traitement en itératif et en récursif. Chacun des deux types de traitement est chronométré avec précision et la durée affichée. On constate qu’effectivement, bien que le code objet en récursif soit plus important en taille, le déroulement de la séquence est plus court. Pour que chaque boucle puisse avoir un travail effectif à réaliser, je me suis contenté de leur faire effectuer une temporisation de 5µS à chaque itération par utilisation de la fonction delayMicroseconds().

Experience_147 : Traitement avec risque.

Accompagnant la Fig.293 les explications présentent une boucle dans laquelle on commence par vérifier si l’on peut effectuer le travail avant de passer à l’action. J’ajoute péremptoirement l’assertion : « Ce type de boucle est à choisir impérativement si l’action peut engendrer un risque« . Avec Experience_147.ino on illustre ce propos. Reprenant une bonne partie du code de P145 on va effectuer une division entière entre X et Y. Hors nous savons que diviser un nombre par zéro est strictement interdit mathématiquement. Il faut donc une procédure récursive qui sera de structure while. Une division par zéro en informatique peut produire n’importe quoi si le programmeur n’a pas paré cette éventualité. Pour tester ce cas, commencer par donner des valeurs quelconques à X et à Y. X peut être égal à zéro, être plus grand ou plus petit que Y. Puis proposez un Y nul. Le programme se bloque et ne réagit plus. Placer la procédure Diviser_X_par_Y() en remarques et valider celle placée entre les deux délimiteurs /* et */. Cette fois les valeurs nulles saisies pour Y sont vérifiées et un texte d’erreur est affiché pour l’opérateur le programme poursuivant son déroulement.

Experience_148 : Factorielle un autre exemple.

Pour illustrer le fait que toute boucle itérative peut être remplacée par une procédure récursive,
Experience_148.ino propose le calcul de la factorielle d’un nombre entier par les deux approches, manipulation qui nous montre un exemple de plus de structure récursive. Nous en avons vu assez pour envisager le dernier exemple qui est un grand classique incontournable.

Experience_149 : Les tours de Hanoî en récursif.

Difficile d’échapper à la vedette incontestée de la récursivité : « Les tours de Hanoï ». Tout étudiant qui poursuit ses études en génie logiciel sera confronté un jour ou l’autre à ce cas typique d’une procédure doublement récursive. Concrètement, c’est un « casse tête » issu d’une légende bouddhiste qui consiste à déplacer n disques de diamètres différents d’une tour de départ à une tour d’arrivée en passant par une tour intermédiaire en un minimum de coups, et en respectant les différentes contrainte suivantes :

• On ne peut déplacer qu’un disque à la fois,
• On ne peut placer un disque que sur un autre disque plus grand que lui ou sur une tour vide.
• Dans l’état initial tous les disques sont placés sur la tour départ le plus grand tout en dessous.
• Dans l’état final tous les disques sont posés sur la tour d’arrivée et dans le même ordre.

La légende prétend que ce sont des moines qui se relient jour et nuit pour résoudre ce problème et que lorsque tous les disques seront déplacés, ce sera la fin du monde !
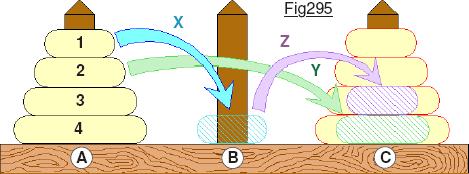Le dessin de la Fig.295 montre un exemple concret pour lequel l’aiguille A est choisie comme tour de départ, C comme tour d’arrivée et B servant de tour intermédiaire. Limité à quatre disques les déplacements X, Y et Z montrent un début de solution qui respecte les contraintes du jeu tel qu’il a été formulé avec précision et rendu public par le mathématicien Français Édouard LUCAS publié en 1892.
ALGORITHME SUGGÉRÉ :
• Il faudra impérativement à un moment donné arriver à placer le disque 4 sur la tour C.
• Il sera donc indispensable de déplacer « Hanoï -1 » sur la tour B.
• Lorsque « Hanoï -1 » se trouve sur la tour B on déplace 4 sur la tour C.
• Il ne reste plus qu’à réaliser encore une fois « Hanoï -1 » de la tour B à la tour C.
Le dessin de la Fig.296 schématise cette stratégie en trois macro-étapes.
Explicité de cette façon la solution envisagée est évidente et simpliste, mais il reste encore le plus délicat à résoudre : Comment réaliser une séquence de type « Hanoï -1 » ?

C’est ici que le serpent va se mordre la queue la réponse étant : Il suffit de réaliser une séquence de type « Hanoï -2 », suivie de « Hanoï -3 » et continuer ainsi jusqu’à ce qu’il ne reste plus un seul disque à déplacer. On décrit ici une solution assez évidente et incontestable, sans pour autant expliciter à chaque fois comment procéder. C’est précisément ce qui sera fait en programmant cette solution par une procédure récursive. Le seul moment ou on explique réellement le travail à faire, c’est lorsque l’on déplace le dernier disque, pour le reste … la récursivité s’en débrouille et c’est toute la magie de ce type d’approche !

Observons la structure de la procédure : En (1) on trouve la déclaration ordinaire d’une procédure qui reçoit quatre paramètres. En (2), tant que l’on n’a pas déplacé tous les disques on continue, c’est le test de sortie de la procédure. En (3) on effectue le Hanoï – 1 de l’Étape n°1. En (4) et (5) on réalise l’Étape n°2. Enfin en (6) on effectue le Hanoï – 1 de l’Étape n°3. L’une des facettes particulières de la récursivité, c’est qu’au final on ne décrit pas le travail global à faire, ici par exemple il n’y a aucune comparaison, calcul etc. On se contente d’afficher.

Durée du traitement. (Pour celle et ceux qui ont du temps.)

Certaines ou certains vont certainement se sentir un peu frustrés parce que le nombre de disques est limité à 32. Vous allez rapidement vous rendre compte qu’au final, ce n’est pas vraiment tragique, car déjà avec ce nombre il y a de quoi vous amuser pas mal de soirées d’hiver si vous le faites à la main. Supposons que vous aidant avec la solution affichée à l’écran pour effectuer un déplacement il vous faut trois secondes. Combien de temps il faudrait pour terminer le jeu ? On montre assez facilement qu’avec cet algorithme, il faut effectuer 2 à la puissance N – 1 opérations pour réaliser tous les transferts et que ce nombre de déplacements est minimal. Il croît très vite avec N, c’est l’histoire du grain de blé sur l’échiquier.

Nous pouvons maintenant apporter une réponse à la question qui était restée en suspend, à savoir le temps que vous allez passer à déplacer les 32 disques. Comme P149 indique à chaque fois le nombre de déplacements et la durée du traitement, pour 16 disques il faut déjà 65535 transferts et il a mis 200541 mS soit 3,0600595mS par déplacement. À cette cadence ultra rapide il lui faut déjà plus de 3min/34S. Vous à raison de 3S par déplacement vous allez attraper mal aux bras et y mettre 54,6 Heures sans manger ni dormir. Alors avec notre limite tristounette de 64 disques il faut 4294961664 déplacements pour la solution optimisée. L’ordinateur va mouliner pendant 13142840389mS soit 2,77 Heures. Et vous 408,5 années sans compter les repas et dodo ! Donc, au final avec 64 disques on couvre assez bien le besoin.

L’explosion numérique des traitements manipulant des nombres avec des puissances exponentielles peut conduire à des temps de traitement prohibitifs rendant le programme inutilisable. (La cryptographie utilise largement ce concept.) Ce n’est pas la seule limite qui bride les applications. Contrairement à ce qui est sans frontière en mathématiques théoriques, nos machines informatiques ont des espaces de travail avec butées, et les nombres qui peuvent être représentés en binaire dans les cellules électroniques sont forcément bornés, tant en positif qu’en négatif, et en nombre de chiffres significatifs. Ces contraintes peuvent ruiner un algorithme qu’il soit itératif ou récursif. Pour tester cette faille logicielle, dans la ligne n°25 de P149 changez le paramètre 32 en 33. Si vous proposez 32 pour Nb le programme fonctionne. Si vous passez à 33 dans son traitement le logiciel arrive quelque part à un nombre qu’il ne peut plus représenter en binaire et provoque une erreur de débordement. (Overflow.)

Experience_150 : Hanoï en itératif.

Toute boucle itérative peut être remplacée par une procédure récursive, c’est juste une question de choix. Si l’on était des machines non influencées par notre vécu, nos habitudes et surtout notre savoir-faire, logiquement, avant de chercher à coder une boucle on devrait effectuer un choix objectif entre itératif et récursif. Réciproquement, toute procédure récursive peut être traitée en itératif, avec parfois plus de complexité. Pour illustrer ce propos je vous propose avec le démonstrateur Experience_150.ino de traiter en Itératif le problème des tours de Hanoï. Au
regard du listage, il est patent qu’en récursif le programme est bien plus complexe. Et encore, on a éliminé le choix des tours et il n’est traité que le cas des nombres de disques PAIRS. Généraliser comme en récursif engendrerait un croquis bien plus long. La procédure itérative utilisée est optimale.
ALGORITHME UTILISÉ :
Soit A, B et C les trois tours, on effectue cycliquement les deux déplacements suivants :
1 : Déplacer le plus petit disque en permutations circulaires de A vers B, de B vers C, de C vers A.
2 : Déplacer un disque sur les deux tours ne contenant pas le plus petit disque :
* Soit le plus petit des deux disques va sur le plus grand,
* Soit une tour est vide, c’est de disque de l’autre tour qui vient sur elle.
• Continuer ces deux déplacements jusqu’à ce toute la tour moins un disque soit déplacée.
• Terminer en déplaçant le dernier disque.
La complexité du logiciel résulte du fait que contrairement à la solution récursive, il faut expliciter en détail chaque action élémentaire.
Présentation du résultat :
Présenté sur la Fig.296 le logiciel commence par se présenter en 1. Puis il saisit en 2 le nombre de disques et l’option d’affichage. En 3 le programme résume les paramètres de l’expérience et précise en 4 le nombre de déplacements optimisés. Tous les affichages de la structure des piles en 5 ne sont affichés que si l’option a été préalablement validée. Il est donc possible de l’activer ou de la suspendre à chaque nouvelle expérience. En 6 les déplacements de type PC sont ceux du mouvement en Permutation Circulaire du plus petit disque. En 7 les lignes commençant par ** sont celles du déplacement entre les deux tours qui n’ont pas le plus petit disque. Enfin en 8 on aboutit au dernier déplacement. Que l’option d’affichage soit validée ou non, dans tous les cas en 9 la structure finale est visualisée. L’expérience se termine en 10 par l’indication du temps nécessaire de traitement pour effectuer tous les déplacements.
Pour 16 disques soit 65535 mouvements il faut 256266mS au programme soit 3,91mS par déplacement. Cette valeur devient stable à partir de 12 Disques. Donc pour le maximum toléré de 32 disque l’ordinateur va mettre environ 4473923 minutes soit 74565 heures c’est à dire 3106 ans s’il n’y a pas de panne ! Dans la pratique on considèrera que cette application n’est pas viable on s’en doute.

REMARQUE : En ligne 65 vous avez un autre exemple de conversion d’une lettre minuscule en son équivalent majuscule, et surtout en ligne 59 l’instruction Impair = Nb & 1 qui positionne le booléen Impair en fonction de la parité du nombre entier Nb.

Déterminer la parité d’un nombre entier.

Faisant appel à l’opérateur logique ET l’instruction Impair = Nb & 1 mérite une petite explication. Commençons par observer en Fig.297 l’écriture des entiers en base deux : On remarque que si le nombre est pair le BIT de poids faible (Situé conventionnellement à droite.) est un « 0« . Au contraire, si l’entier est impair sont BIT de poids faible est un « 1« . Aussi, le plus simple pour déterminer la parité d’un nombre consiste à « isoler » son BIT de poids faible. Pour alléger le didacticiel le chapitre relatif aux masques logiques est détaillé dans le document Les masques logiques.pdf que je vous invite à consulter en préalable à ces explications. Ici le masque logique vaut 0001 et de ce fait annule avec le & tous les BITs de poids fort sauf celui de poids faible. En fonction de la parité le résultat sera 0000 ou 0001 qui translaté à un booléen sera traduit comme false ou true.

Experience_151 : Un petit défi.

Toute boucle itérative peut être remplacée par une procédure récursive, c’est juste une question de choix, sert de préambule à P150. Pour ce démonstrateur je propose de soumettre à votre sagacité la transformation de la boucle itérative d’Experience_151.ino en son équivalent récursif. Pour ne pas que votre regard soit par inadvertance trop attiré par la solution, je vous propose cette dernière dans le dossier <! Petits PROJETS>. Le programme saisit deux nombres entiers X et Y. Il faut en déduire la valeur de X élevé à la puissance Y. Pour élever un nombre X à la puissance Y il faut le multiplier Y fois par lui-même. Exemple : 3 puissance 5 = 3 x 3 x 3 x 3 x 3 = 243. Attention, la solution que je vous propose ne pare pas le danger potentiel d’un résultat « explosif » risque encouru chaque fois que l’évolution est exponentielle. (Si le calcul déborde les possibilités de codage binaire le programme affiche « inf » pour INFINI. Pour la solution c’est plus sournois car il n’y a pas de message d’erreur mais le résultat est faux !) C’est à vous de jouer …

La suite est ici.