Dans ce tutoriel, je vais vous apprendre à convertir du :
- Décimal au binaire et à l'hexadécimal.
- Binaire au décimal et à l'hexadécimal.
- Hexadécimal au décimal et au binaire.
C'est très simple une fois la méthode acquise !
Mais n'attendons pas, commençons à attaquer tout de suite !
Sommaire :
1. Du décimal vers le binaire
2. Du décimal vers l'hexadécimal
3. Du binaire au décimal
4. De l'hexadécimal au décimal
5. De l'hexadécimal au binaire
6. Du binaire à l'hexadécimal
7. Grand exercice
Du décimal vers le binaire
Pour convertir du décimal vers le binaire, il faut additionner toutes les puissances de 2 que contient le chiffre en commençant par la plus grande pour retomber à ce chiffre.
Ma phrase étant assez compliquée (j'explique très mal >.<), je vais tout de suite vous montrer un exemple.
Tout d'abord, rappelons quelques puissances de 2 pour nous aider :
Convertissons 563 en binaire :
La puissance de 2 la plus proche que peut contenir 563 est 512.
Ensuite il faut trouver la somme des puissances de deux qui font 563 en commençant par la plus grande (ici 1024 serait inutile comme il est trop grand, on commence donc par 512).
Revenons donc à nos moutons chiffres :
563 = 512*1 + 256*0 + 128*0 + 64*0 + 32*1 + 16*1 + 8*0 + 4*0 + 2*1 + 1*1
Voila ! On sait maintenant que 563 en binaire est 1000110011, car il contient 1 fois 512, 0 fois 256, 0 fois 128, 0 fois 64, 1 fois 32, etc... Facile !
Essayons avec 84 ; la base la plus proche et en dessous de 84 est 64. on commence donc par 64 :
64*1 + 32*0 + 16*1 + 8*0 + 4*1 + 2*0 + 1*0.
84 = 1010100.
Pour vous entrainer, convertissez : 1589, 27, 89, 61 et 985 en binaire, réponses en fin de cour !
Du décimal vers l'hexadécimal
Pour convertir du décimal vers l'hexadécimal, il faut chercher combien de fois il y a la puissance de 16 la plus proche dedans.
Encore une fois, je doute que vous ayez tout compris du premier coup, donc venons en à la pratique.
Voici un petit tableau avec les principales puissances de 16 (tableau très petit vous verrez ).
).
Ensuite, il est très important de savoir que que l'hexadécimal va de 0 à 15 mais que à partir de 10, on compte avec les premières lettres de l'alphabet.
Voici l'hexadécimal de 0 à 15 : 0 1 2 3 4 5 6 7 8 9 A B C D E F
Passons maintenant à la pratique, convertissons 563 :
La puissance de 16 la plus proche de 563 et qui est plus petite que 563 est 256 ; on cherche combien de fois il y a 256 dans 563 : 2 fois.
Ensuite on cherche combien de fois il y a 16 (la puissance en dessous de 256) dans le reste de 563-2*256 (=51) : 3 fois.
Enfin, on cherche combien de fois il y a 1 (la puissance en dessous de 16) dans le reste : 3.
Donc, 563 en décimal est égal à 233 en hexadécimal.
Un autre exemple pour mieux comprendre, convertissons 3596 :
3596 = 256*14 + 0*16 + 12 ; donc 3596 = E0C.
Pour vous entrainer, convertissez : 52 653, 2016, 56 et 25 062, corrigé en fin de cour !
Du binaire au décimal
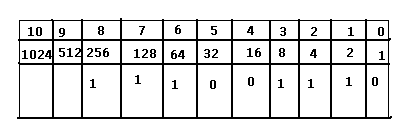
Imaginons que l'on vous donne 111001110 à convertir en décimal, comment faire ? Regardez :
Comme vous pouvez le voir, il vous suffit de faire un tableau et d'y placer les chiffres en partant de la droite vers la gauche. Ensuite, il faut additionner là où il y a des 1 dans la tableau, ici cela nous donne : 2 + 4 + 8 + 64 + 128 + 256 = 462.
Nota : Vous pouvez aussi utiliser ce tableau pour convertir du décimal au binaire, en plaçant un 1 dedans dès qu'il y a une puissance de 2 à ajouter ; essayez !
Essayer de traduire : 1001101, 1010101001, 11111, 10100001, corrigé en fin de cours !
De l'hexadécimal au décimal
Alors là, c'est très simple, imaginons que nous voulons traduire 956 en décimal, il faut additionner les puissances de 16 une à une en partant de la droite, ici, 956 = 1*6 + 16*5 + 256*9 = 2390 !
Pour vous entrainer, essayez de convertir : F05, 256, 9B6 et ACE, corrigé en fin de cours !
De l'hexadécimal au binaire
C'est encore une fois, très simple, il faut traduire chiffre après chiffre, en partant de la gauche, du décimal au binaire. Mais, qu'est ce que le décimal vient faire ici me direz vous ? C'est très simple, regardez :
Pour traduire 563 (qui est en hexadécimal), en binaire, il faut traduire 5 en binaire, 6 en binaire et 3 en binaire et placer tout cela un à côté de l'autre !
Donc pour 563 : 5 = 101, 6 = 110 et 3 = 11,
donc 563 en hexadécimal est égal à 10111011 en binaire ! => C'est FAUX, il faut toujours faire des "paquets de 4", c'est à dire que dès qu'un paquet est plus petit, il faut lui rajouter des 0 devant pour qu'il fasse une taille de 4, donc 563 en binaire = 010101100011, et encore ici, la méthode dit qu'il ne faut pas faire un groupement de 4 pour la première particule de la gauche, on doit donc enlever le premier 0, finalement, 563(hexadécimal) = 10101100011 !
Ca parait compliqué mais en réalité c'est simple !
Essayons avec 2E3 : 9 = 10, E = 1110 et 3 = 11, ici, on ne doit pas rajouter de zéro au premier membre, donc il reste 10, le second fait déjà un paquet de 4, donc on ne touche à rien, et le dernier ne fait qu'un paquet de 2, donc on rajoute 2 zéros devant, donc 2E3(hexadécimal) = 1011100011 !
Essayez de traduire : EFB, 256, 532 et 2F !
Réponses en fin de cours !
Du binaire à l'hexadécimal
C'est tout simplement l'inverse que pour de l'hexadécimal au binaire !
On prend des paquets de 4 en commençant par la droite et on converti en décimal !
Par exemple, prenons 101110110, faisons les paquets de 4 : 1(il est tout devant et n'a pas besoin de 0 en plus), 0111 et 0110.
1 = 1, 0111 = 7 et 0110 = 6, donc 101110110 = 176(hexadécimal).
Pour vous entrainer, traduisez : 100110, 1110110 et 1101.
Grand exercice
Pour "finaliser" votre apprentissage, essayez de traduire ceci :
- 674(décimal) à traduire en binaire et en hexadécimal ;
- 1011101010 à traduire en décimal et en hexadécimal ;
- 1F2(hexadécimal) à traduire en décimal et binaire.
Je donne toutes les réponses dans la partie suivante !
CORRECTIONS
1- Exercice du 1) :
1589 = 11101000011 ;
27 = 11011 ;
89 = 1011001;
61 = 111101;
985 = 1111011001.
2- Exercice du 2) :
52 653 = CDAD;
2016 = 7E0;
56 = 38;
25 062 = 61E6;
3- Exercice du 3) :
1001101 = 77;
1010101001 = 681;
11111 = 31;
10100001 = 161;
4- Exercice du 4) :
F05 = 3845;
256 = 598;
9B6 = 2486;
ACE = 2766;
5- Exercice du 5) :
EFB = 111011111011;
256 = 1001010110;
532 = 10100110010;
EF = 11101111;
6- Exercice du 6) :
100110 = 26;
1110110 = 76;
1101 = D;
7- Grand exercice :
674(décimal) = 1010100010 et 2A2.
1011101010 = 746(décimal) et 2EA.
1F2 = 498 et 111110010.
Voila, ici s'achève le tutoriel, certes long, mais très facile à comprendre avec un peu d'entrainement !
Surtout n'hésitez pas à venir faire vos critiques sur le forum pour m'aider à mieux rédiger ! Et si vous ne comprenez pas quelque chose (ou si vous trouvez une faute o_O ), envoyez moi un message privé !
Merci d'avoir lu jusqu'au bout !
- Décimal au binaire et à l'hexadécimal.
- Binaire au décimal et à l'hexadécimal.
- Hexadécimal au décimal et au binaire.
C'est très simple une fois la méthode acquise !
Mais n'attendons pas, commençons à attaquer tout de suite !
Sommaire :
1. Du décimal vers le binaire
2. Du décimal vers l'hexadécimal
3. Du binaire au décimal
4. De l'hexadécimal au décimal
5. De l'hexadécimal au binaire
6. Du binaire à l'hexadécimal
7. Grand exercice
Du décimal vers le binaire
Pour convertir du décimal vers le binaire, il faut additionner toutes les puissances de 2 que contient le chiffre en commençant par la plus grande pour retomber à ce chiffre.
Ma phrase étant assez compliquée (j'explique très mal >.<), je vais tout de suite vous montrer un exemple.
Tout d'abord, rappelons quelques puissances de 2 pour nous aider :
| 2 puissance ... | Est égal à ... |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
Convertissons 563 en binaire :
La puissance de 2 la plus proche que peut contenir 563 est 512.
Ensuite il faut trouver la somme des puissances de deux qui font 563 en commençant par la plus grande (ici 1024 serait inutile comme il est trop grand, on commence donc par 512).
Revenons donc à nos moutons chiffres :
563 = 512*1 + 256*0 + 128*0 + 64*0 + 32*1 + 16*1 + 8*0 + 4*0 + 2*1 + 1*1
Voila ! On sait maintenant que 563 en binaire est 1000110011, car il contient 1 fois 512, 0 fois 256, 0 fois 128, 0 fois 64, 1 fois 32, etc... Facile !
Essayons avec 84 ; la base la plus proche et en dessous de 84 est 64. on commence donc par 64 :
64*1 + 32*0 + 16*1 + 8*0 + 4*1 + 2*0 + 1*0.
84 = 1010100.
Pour vous entrainer, convertissez : 1589, 27, 89, 61 et 985 en binaire, réponses en fin de cour !
Du décimal vers l'hexadécimal
Pour convertir du décimal vers l'hexadécimal, il faut chercher combien de fois il y a la puissance de 16 la plus proche dedans.
Encore une fois, je doute que vous ayez tout compris du premier coup, donc venons en à la pratique.
Voici un petit tableau avec les principales puissances de 16 (tableau très petit vous verrez
| 16 puissance ... | Est égal à ... |
| 0 | 1 |
| 1 | 16 |
| 2 | 256 |
| 3 | 4096 |
Ensuite, il est très important de savoir que que l'hexadécimal va de 0 à 15 mais que à partir de 10, on compte avec les premières lettres de l'alphabet.
Voici l'hexadécimal de 0 à 15 : 0 1 2 3 4 5 6 7 8 9 A B C D E F
Passons maintenant à la pratique, convertissons 563 :
La puissance de 16 la plus proche de 563 et qui est plus petite que 563 est 256 ; on cherche combien de fois il y a 256 dans 563 : 2 fois.
Ensuite on cherche combien de fois il y a 16 (la puissance en dessous de 256) dans le reste de 563-2*256 (=51) : 3 fois.
Enfin, on cherche combien de fois il y a 1 (la puissance en dessous de 16) dans le reste : 3.
Donc, 563 en décimal est égal à 233 en hexadécimal.
Un autre exemple pour mieux comprendre, convertissons 3596 :
3596 = 256*14 + 0*16 + 12 ; donc 3596 = E0C.
Pour vous entrainer, convertissez : 52 653, 2016, 56 et 25 062, corrigé en fin de cour !
Du binaire au décimal
Imaginons que l'on vous donne 111001110 à convertir en décimal, comment faire ? Regardez :
(La première sont les puissances de 2 et la seconde sont les nombres qui leurs correspondent).
Comme vous pouvez le voir, il vous suffit de faire un tableau et d'y placer les chiffres en partant de la droite vers la gauche. Ensuite, il faut additionner là où il y a des 1 dans la tableau, ici cela nous donne : 2 + 4 + 8 + 64 + 128 + 256 = 462.
Nota : Vous pouvez aussi utiliser ce tableau pour convertir du décimal au binaire, en plaçant un 1 dedans dès qu'il y a une puissance de 2 à ajouter ; essayez !
Essayer de traduire : 1001101, 1010101001, 11111, 10100001, corrigé en fin de cours !
De l'hexadécimal au décimal
Alors là, c'est très simple, imaginons que nous voulons traduire 956 en décimal, il faut additionner les puissances de 16 une à une en partant de la droite, ici, 956 = 1*6 + 16*5 + 256*9 = 2390 !
Pour vous entrainer, essayez de convertir : F05, 256, 9B6 et ACE, corrigé en fin de cours !
De l'hexadécimal au binaire
C'est encore une fois, très simple, il faut traduire chiffre après chiffre, en partant de la gauche, du décimal au binaire. Mais, qu'est ce que le décimal vient faire ici me direz vous ? C'est très simple, regardez :
Pour traduire 563 (qui est en hexadécimal), en binaire, il faut traduire 5 en binaire, 6 en binaire et 3 en binaire et placer tout cela un à côté de l'autre !
Donc pour 563 : 5 = 101, 6 = 110 et 3 = 11,
Ca parait compliqué mais en réalité c'est simple !
Essayons avec 2E3 : 9 = 10, E = 1110 et 3 = 11, ici, on ne doit pas rajouter de zéro au premier membre, donc il reste 10, le second fait déjà un paquet de 4, donc on ne touche à rien, et le dernier ne fait qu'un paquet de 2, donc on rajoute 2 zéros devant, donc 2E3(hexadécimal) = 1011100011 !
Essayez de traduire : EFB, 256, 532 et 2F !
Réponses en fin de cours !
Du binaire à l'hexadécimal
C'est tout simplement l'inverse que pour de l'hexadécimal au binaire !
On prend des paquets de 4 en commençant par la droite et on converti en décimal !
Par exemple, prenons 101110110, faisons les paquets de 4 : 1(il est tout devant et n'a pas besoin de 0 en plus), 0111 et 0110.
1 = 1, 0111 = 7 et 0110 = 6, donc 101110110 = 176(hexadécimal).
Pour vous entrainer, traduisez : 100110, 1110110 et 1101.
Grand exercice
Pour "finaliser" votre apprentissage, essayez de traduire ceci :
- 674(décimal) à traduire en binaire et en hexadécimal ;
- 1011101010 à traduire en décimal et en hexadécimal ;
- 1F2(hexadécimal) à traduire en décimal et binaire.
Je donne toutes les réponses dans la partie suivante !
CORRECTIONS
1- Exercice du 1) :
1589 = 11101000011 ;
27 = 11011 ;
89 = 1011001;
61 = 111101;
985 = 1111011001.
2- Exercice du 2) :
52 653 = CDAD;
2016 = 7E0;
56 = 38;
25 062 = 61E6;
3- Exercice du 3) :
1001101 = 77;
1010101001 = 681;
11111 = 31;
10100001 = 161;
4- Exercice du 4) :
F05 = 3845;
256 = 598;
9B6 = 2486;
ACE = 2766;
5- Exercice du 5) :
EFB = 111011111011;
256 = 1001010110;
532 = 10100110010;
EF = 11101111;
6- Exercice du 6) :
100110 = 26;
1110110 = 76;
1101 = D;
7- Grand exercice :
674(décimal) = 1010100010 et 2A2.
1011101010 = 746(décimal) et 2EA.
1F2 = 498 et 111110010.
Voila, ici s'achève le tutoriel, certes long, mais très facile à comprendre avec un peu d'entrainement !
Surtout n'hésitez pas à venir faire vos critiques sur le forum pour m'aider à mieux rédiger ! Et si vous ne comprenez pas quelque chose (ou si vous trouvez une faute o_O ), envoyez moi un message privé !
Merci d'avoir lu jusqu'au bout !