Hmmm, je remonte un peu ce topic avec des explications.
Le problème auquel tu es confronté est un problème
d'approximation de fonction: quelle est la relation entre tes valeurs de commande et l'angle de sortie du servomoteur ?
Idéalement, c'est une relation linéaire: à une valeur de commande correspond un angle, et cette relation évolue proportionnellement : si je double ma commande, je double mon angle de sortie.
Dans l'exemple que tu donnes, on peut identifier:
- l'espace mathématique d'entrée T (pour Theta, les angles en degrés, un espace de dimension 1 à valeurs dans le sous-espace des nombres réels R borné [-180.0,180.0])
- l'espace mathématique de sortie C (pour Commande, les commandes de ton servomoteur envoyées par ton µC, en int)
- la fonction f, qui définit la relation T -> C.
Pour l'instant, tu avais fait l'hypothèse (peut-être non-consciemment) que cette fonction f était linéaire. Donc que pour theta dans l'espace THETA (c'est-à-dire pour une valeur angulaire entre -180 et 180), la commande 'com' à appliquer vaut :
com = a * theta + b
C'est ce qui se passe quand tu fais 'map'.
Mais ton constat, c'est que cette hypothèse n'est pas assez satisfaisante: quand tu appliques 'com' sur ton servo, tu ne vas pas à 'theta' mais à 'theta' + 'erreur'.
En soi, ça n'est pas surprenant: les composants réels sont toujours un peu éloignés de leur modèle mathématique idéal. Dans ce cas, il faut évaluer à quel point le modèle linéaire est faux, donc faire des mesures: où va mon servo quand je lui applique la commande c ?
Avec ces points, tu vas voir la tête qu'à cette fonction f. Et si le modèle linéaire est une bonne approximation de cette fonction ou pas.
Quand tu appliques la solution de Mike (faire une multimap), ça consiste à passer d'un modèle linéaire à un modèle
linéaire par parties pour f. Au lieu d'utiliser une seule droite, tu approches tes points avec une droite entre [-180, p0], une autre droite entre [p0, p1], etc.
Et dans ce cas, il faut se poser deux questions : est-ce que ça vaut vraiment le coup de passer à un modèle plus complexe? Si oui, comment découper la fonction ?
Il faut considérer le gain en précision opposé à la complexité de l'approximateur (le nombre de paramètres à trouver, ici les bornes des intervalles et les coefficients des droites).
Voici un petit exemple en considérant que les points de ton premier post sont les points mesurés sur ton servo (donc les relations que tu veux obtenir). On va d'abord regarder la tête de ces points.
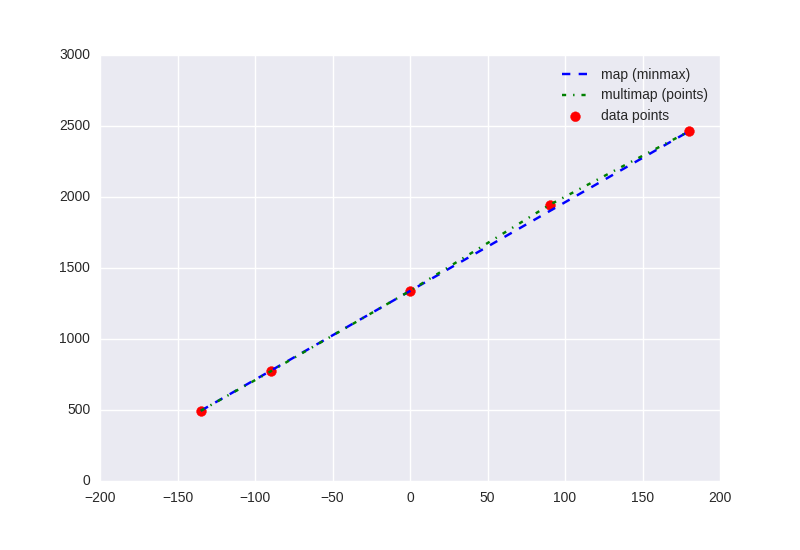
À première vue, difficile de détecter une différence entre l'approximation linéaire (juste avec le min et le max et map, en bleu) et l'approximation linéaire par parties (en vert).
Vu qu'on ne peut pas conclure sur l'intérêt d'utiliser une approximation linéaire par parties juste visuellement, on va calculer l'erreur que produit l'approximation linéaire simple.
On commence par estimer, à partir des points extrêmes (min et max), les coefficients du modèle linéaire (donc les coeff a et b de a fonction). On calcule en fait deux approximations: en estimant b à partir du min ou du max.
En utilisant ces coefficients, on peut prédire la commande à appliquer pour obtenir certaines valeurs d'angle (voir l'équation plus haut). Du coup, pour chaque point mesuré, on calcule la commande prédite par notre modèle et on calcule l'erreur avec la valeur mesurée. Ici, on peut voir que nos modèles linéaires sont bons à un des extrêmes (celui quo'n a utilisé pour calculer

, mais que plus on s'éloigne de l'extrême, plus l'erreur augmente.
Le modèle 1 reste globalement correct (erreur maximale 5%), le modèle 2 atteint parfois 15% d'erreur. En pratique, est-ce que le modèle 1 est suffisant dépend de l'application (donc si 5% d'erreur est acceptable dans le système).
Je m'arrête là pour le moment, n'hésitez pas si vous avec des questions ou vous voulez des précisions !
Tous les calculs sont dispos dans ce notebook jupyter :
https://github.com/r...oximation.ipynbPlus d'infos sur l'approximation linéaire d'un ensemble de points :
http://grasland.script.univ-paris-diderot.fr/STAT98/stat98_7/stat98_7.htm





















