Bonjour,
Ben oui Forthman, c'est dit autrement mais j'adapte mes explications en fonction de vos réponses pour vous communiquer la finalité correctement. Je pense ma position respectueuse vis à vis du forum. Quant aux réponses qui ne pourraient pas me plaire, croyez moi, j'ai dépassé ce stade et garde un esprit ouvert.
Il y a un problème de communication: Pour moi optimiser les pertes c'est les rendre plus efficaces, alors que pour toi c'est les rendre le moins efficace possible, ce auquel j'adhère. J'ai écris (réduire la réactance) j'aurais du écrire (réduire ces effets négatifs). Important je n'ai pas écris que la réactance était négative, car c'est un phénomène d'induction qui nous permet d'obtenir le courant induit.
Je sais que les pertes sont importantes. Cependant, dans un exemple comme la roue de Falkirk, il y a des engrenages dont les pertes n’empêchent pas le fonctionnement très avantageux, ou les engrenages des éoliennes.
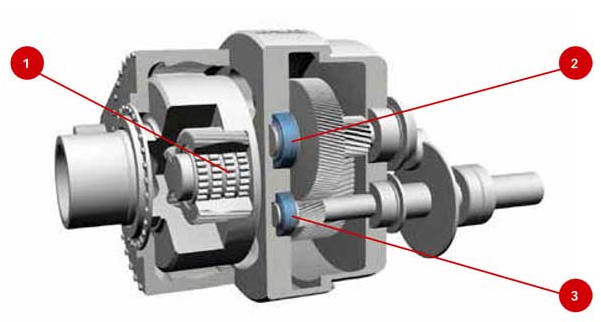
Je n’ai pas réussi à n’utiliser qu’un seul axe de charge. Je jette l’éponge et je m’arrange avec les deux axes de charges.
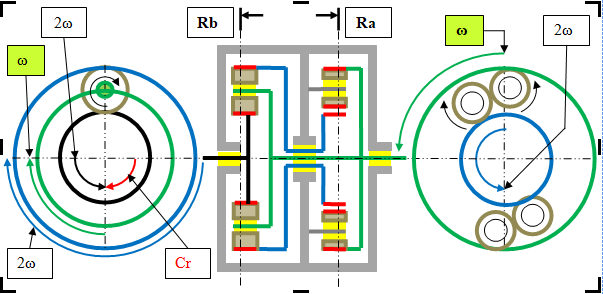
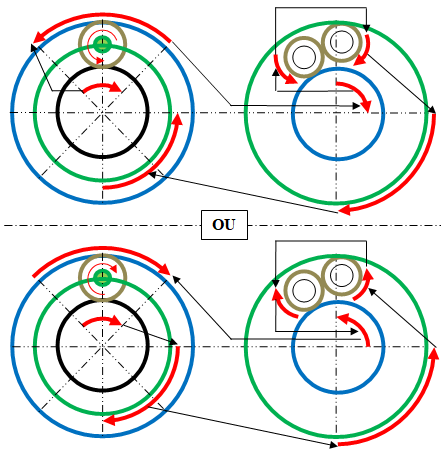
Je travaille donc avec deux axes recevant la même charge et tournant dans le même sens à des vitesses de rotation différentes. Je garde le rapport ½ du différentiel de rotation (≠ω) qui me sera utile par la suite.
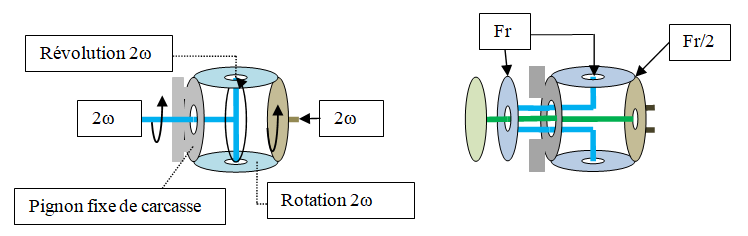
Pour avoir la possibilité du rapport ½ avec le réducteur épicycloïdal, je suis les recommandations de Forthamn avec le porte-satellites fixe sur la carcasse.
Pour avoir le même sens de rotation entre la couronne et le planétaire, je double les satellites sur le même porte-satellites fixe.
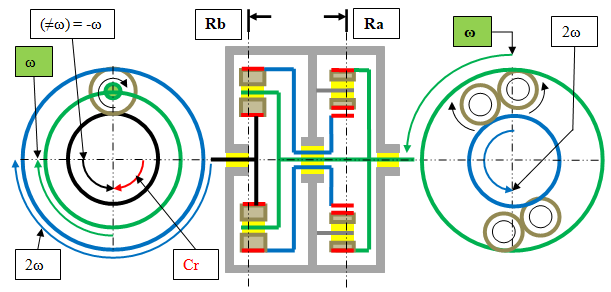
Résumé : Rapport ½ en rotation avec le même sens de rotation et un (≠ω = à ω).
Le couple moteur peut faire tourner les axes de charge.
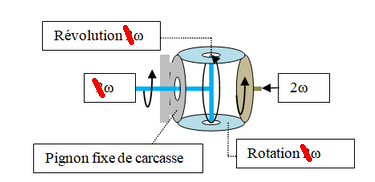
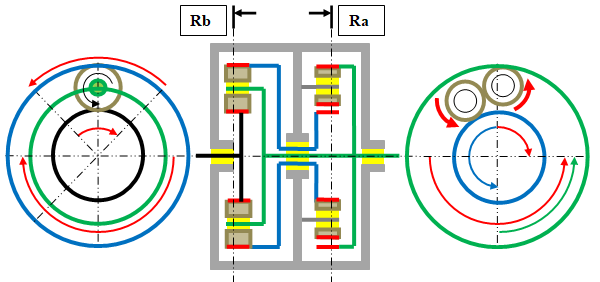
Si une charge (ou réaction) applique deux forces égales et opposées, sur chacun des axes de charge. Ces deux forces (flèches rouge) s’équilibreront inévitablement sur les deux satellites.
C’est mathématique, en considérant les sens de rotation des couples que ces forces imposeront sur les axes de charges, je peux écrire la formule des sens ainsi :
Couple moteur = (2+) et couples opposés sur les axes de charge = (1+) + (1-).
Ce qui donne => Σ = (2+) + [(1+) + (1-)] = (2+)
Ou couple moteur = (+) en conséquence Σ = (+) + [(1+) + (1-)] = (+)
Car si l’opposition est composée de deux couples égaux et opposés, inévitablement l’un des deux couples aura l’un des sens du couple moteur. Pour l’instant je raisonne (relativement) en statique.
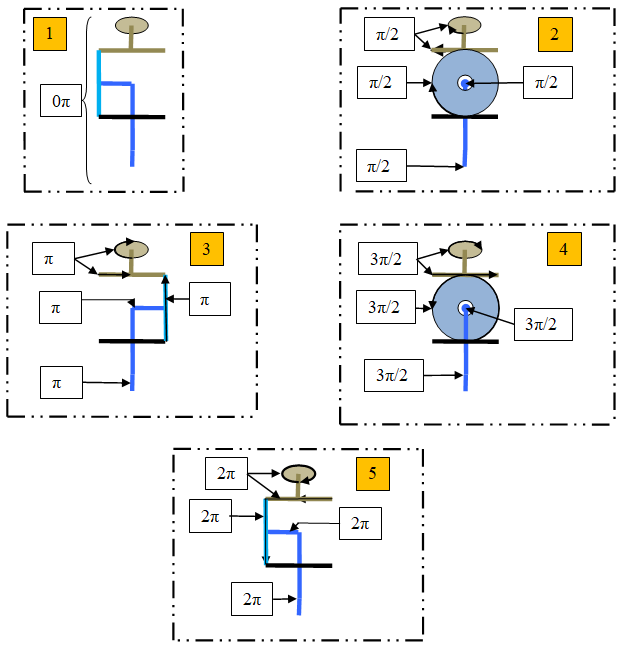
Si l’image n’est pas asse explicite, je la compléterais.
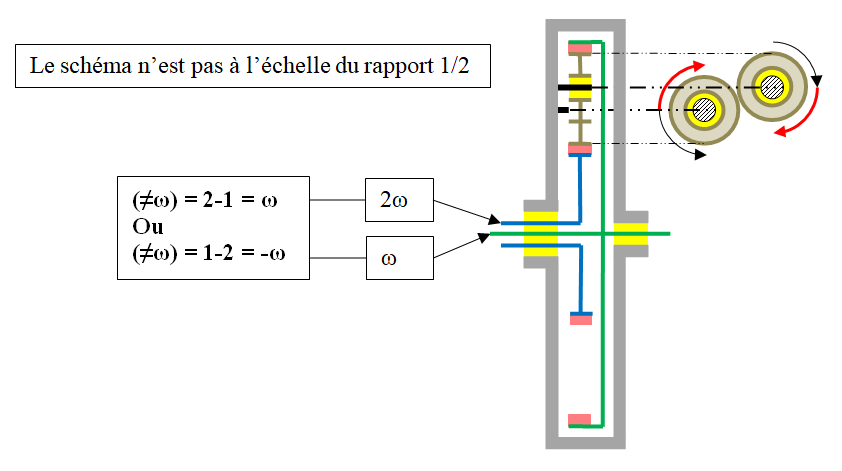
De sorte que le couple moteur peut faire tourner l’ensemble des deux axes de charge sans être influencer par la charge. Il me faut donc pour récupérer ce (≠ω) du couple moteur, qui s’exprime sur les axes vert et bleu, que la charge (ou réaction) s’oppose à ce (≠ω).
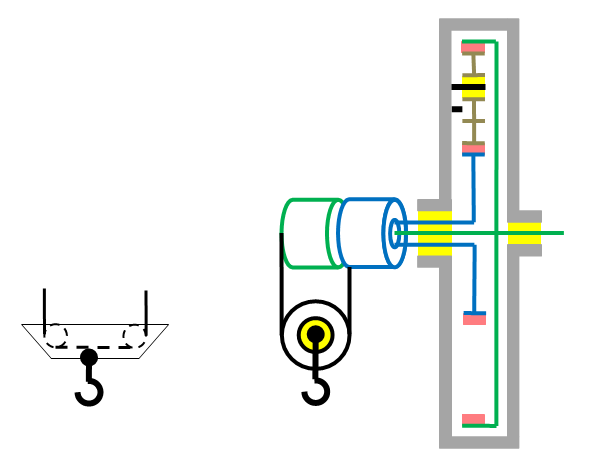
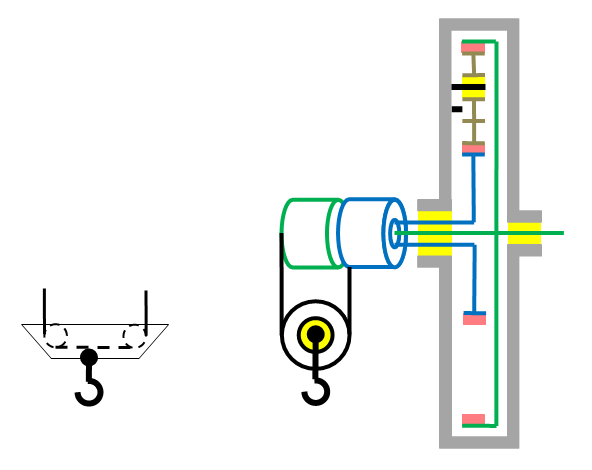
Pour cela en première application j’utilise un treuil double dont les axes sont solidaires des axes de charge bleu est vert. Ainsi la charge est divisée en deux forces égales et opposées.
Les câbles doivent impérativement attaquer chaque treuil, de façon que les deux forces égales et opposées, se retrouvent respectivement sur chaque axe de charge diamétralement opposé.
Ainsi la charge même suspendue et sans couple moteur, est incapable de faire tourner l’axe moteur. Donc auto-équilibrage de la charge automatique quelque soit sa valeur.
Je suis toujours tributaire de la distance et de la gravité.
Quelque soit le sens de rotation, les explications précédentes restent valables. Ma réflexion pour la situation dynamique est la suivante :
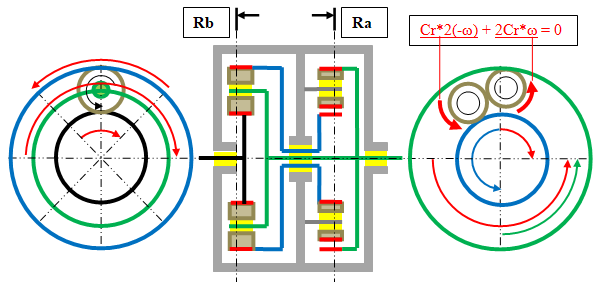
Le signe (+) ou (-) de l’énergie développée par les deux forces résistantes se détermine en fonction du sens de rotation du couple moteur ou autrement écrit, de la montée ou de la descente. Sur les axes de charge (à couple réactif égaux) nous avons une énergie développée deux fois supérieure sur l’axe qui tourne à (2ω).
Résultat en situation dynamique le couple moteur devrait assumer la moitie de la charge.
Car la somme des puissances de réaction dans le réducteur est alors :
Σ = (+P) + (-2P) = (+P). Ici P représente la puissance de la résistance de charge en mouvement divisée par 3. Un P sur l’axe le plus lent et deux P sur l’axe le plus rapide.
Ma déduction est-elle exacte ?
Dans ce cas je dois diviser par deux le couple réactif de l’axe bleu, tout en gardant la même vitesse. Je pense avoir la solution. Je la prépare et vous en fait par. Cependant si je me trompe et qu’en régime dynamique vous en déduisez que la réaction sera auto-équilibrée, Dite le moi s’il vous plait.
![]()