Dans ce tutoriel, je vais vous expliquer une méthode alternative pour simplifier vos équations logiques.
Si vous avez du mal avec les simplifications faites "à la main", alors ce tutoriel est fait pour vous car la méthode est assez simple et efficace à 100%.
La table de vérité
Tout d'abord sachez que le plus couramment vous rencontrerez des tables de vérité avec 4 entrées ; les tables avec plus d'entrées sont plus rares, en général.
Je vais donc ici vous exposer une table de vérité avec 4 variables d'entrées et 2 sorties ; je vous montrerez quand même, par la suite, un tableau de Karnaugh avec 5 variables d'entrées.
Soit la table de vérité suivante, avec a, b, c et d comme variables d'entrée et S1 et H1 comme variables de sortie. Comme il y a 4 variables d'entrée, il faut 2^4 (16) lignes, allant du 0 binaire, au 15 binaire ; en sachant que les 0 ou les 1 veulent dire "ouvert" ou "fermé".
 Les "X" sont les impossibilités technologiques, c'est à dire que c'est un état impossible à réaliser dans la réalité ; comme par exemple un capteur qui détecte une pièce trop grande et un capteur qui détecte une pièce trop petite activés en même temps. Ces impossibilités nous seront quand même utiles plus tard.
Les "X" sont les impossibilités technologiques, c'est à dire que c'est un état impossible à réaliser dans la réalité ; comme par exemple un capteur qui détecte une pièce trop grande et un capteur qui détecte une pièce trop petite activés en même temps. Ces impossibilités nous seront quand même utiles plus tard.
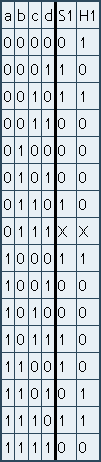
Vous pouvez déjà observer que j'ai placé une impossibilité technologique à la 8ième ligne.
Il faut maintenant établir les équations de nos sorties, c'est à dire, écrire la valeur de a, b, c et d quand la sortie vaut 1. Si la sortie vaut 1 et que a vaut 0 par exemple, on notera alors .
.
S1 =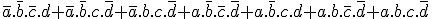
S2 =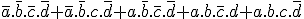
 Rappel : le symbole '.' signifie "et" et le symbole '+' signifie "ou".
Rappel : le symbole '.' signifie "et" et le symbole '+' signifie "ou".
Vous pouvez aussi constater que les impossibilités technologiques ne sont pas représentées dans l'équation.
Le tableau de Karnaugh
Voici à quoi doit ressembler le tableau de Karnaugh vide pour S1 dans notre cas :
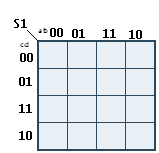
Nous pouvons constater que :
- Le tableau contient 16 cases, 4 colonnes (variables a et * 4 lignes (variables c et d).
* 4 lignes (variables c et d).
- Les cases sont "numérotées" en ne faisant changer qu'une seule variable à la fois => 00, 01, 11, 10 ; une seule variable est modifiée à chaque fois.
- Dans les colonnes, 00 signifie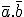 , 01 signifie
, 01 signifie 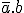 , 11 signifie a.b et 10 signifie
, 11 signifie a.b et 10 signifie 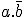 .
.
- Dans les lignes, c'est pareil, 00 =>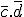 , 01 =>
, 01 => 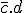 , 11 => c.d et 10 =>
, 11 => c.d et 10 => 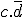 .
.
Maintenant, nous pouvons remplir notre tableau ; je vous met l'exemple tout de suite pour mieux comprendre.
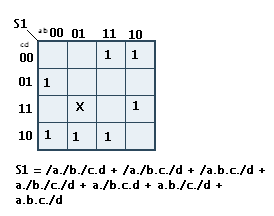
Comment l'ais-je rempli ? C'est simple, la première expression est : /a./b./c.d, j'ai donc pris dans le tableau la colonne 00 (/a./ et la ligne du 01 (
et la ligne du 01 (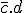 ) et j'y est mis un 1 dedans. Il faut répéter cette action pour tous les morceaux de l'équation.
) et j'y est mis un 1 dedans. Il faut répéter cette action pour tous les morceaux de l'équation.
Vous avez aussi pu remarquer que maintenant j'ai placé l'impossibilité technologique (le "X") dans le tableau ; il va nous servir pour la simplification.
Venons en à la simplification :
S1 (non simplifié) =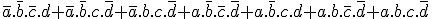 .
.
S1 (simplifié) =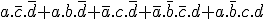 .
.
Mais comment ais-je trouvé cela ? C'est très simple, regardez :
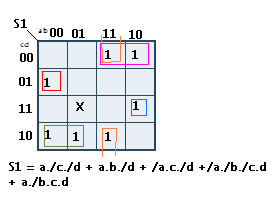
La méthode et les règles :
- Cette méthode ne marche que si l'équation ne comporte pas de parenthèses ni de barre sur plusieurs variables ! Si vous avez des parenthèses, développez d'abord pour ne plus en avoir, et si vous avez une barre sur plusieurs éléments, utilisez le théorème de De Morgan.
- Regroupez les "1" par paquets de puissance de 2 (1,2,4,8,16...) ;
- Il faut vous imaginer le tableau comme une sphère, c'est à dire que un "1" étant placé tout en haut à droite pourra se regrouper avec un "1" placé tout en haut à gauche ou bien avec un "1" placé tout en bas à droite ;
- Il est interdit de faire des groupements en diagonale, donc il n'y a que des groupements carrés et rectangles ;
- Pour que l'équation soit simplifiée au maximum, il faut que tous les "1" soient englobés dans le plus grand groupement possible, vous pouvez "utiliser" plusieurs fois le même un si il permet de faire un plus grand groupement avec d'autres 1 (cf. le rose et le orange de S1 par exemple) ;
- Il faut séparer vos groupement d'équation par un "ou" (le symbole "+") ;
- Regardez si les impossibilités technologiques vous permettent de faire un plus grand paquet (dans notre cas il n'y avait qu'une seule impossibilité et elle ne nous permettait pas de faire un paquet plus grand), de plus, il ne faut pas faire de paquet avec les impossibilités technologiques ;
- Ne prenez que l'état des variables qui ne changent pas, par exemple, observons le groupement de couleur orange : comme le tableau est sphérique, le 1 en haut et le 1 en bas sont sensés se toucher, et comme il n'y a pas de 1 permettant de faire un groupement plus grand, le groupement sera de deux ; ensuite, nous pouvons que pour le groupement observé, sur les colonnes, le 1 est placé sur la 3ième colonne où a et b valent 1 et sur la première et dernière ligne où c et d valent respectivement 0 et 0 et 1 et 0. Pour a et b, pas de problème, les deux variables valent 1 tout le temps, le bout d'équation est donc a.b, mais pour c et d, seulement le c change, donc il faut l'ignorer, on ne garde que le d qui vaut toujours 0 ; le bout d'équation complet est donc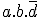 .
.
Répétez cette action pour tous les groupements et vous aurez votre équation simplifiée au maximum ! Si vous avez des 1 avec lesquels il est impossible de faire un groupement, alors faite comme si il était dans un groupement, notez l'équation des valeurs des variables qui ne changent pas, pour un 1 seul, aucune variable ne changera donc. (Par exemple, avec le "1 rouge", a et b valent tous les deux 0 et c et d valent 0 et 1, le bout d'équation est donc :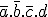 .
.
Il est parfois possible de faire des groupements différents mais les résultats seront simplifiés au mêmes degrés.
Maintenant, je vous laisse réfléchir pour H1 ! Je vous met la réponse ci dessous.
Surtout n'hésitez pas à relire, au début ça semble difficile alors que en fait, c'est très simple.
(De plus, je ne suis pas très bon pédagogue :| ).
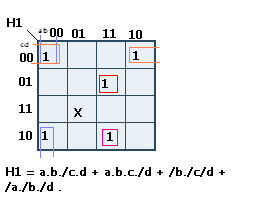
Solution de H1 :
Autre exemple
Soit l'équation suivante :
S =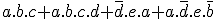 .
.
On peut déjà constater qu'il y a cinq variables et non plus quatre !
Voici à quoi ressemble une table de Karnaugh avec cinq entrées :
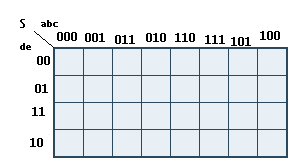
Vous pouvez constater que j'ai mis a,b et c sur les colonnes et d et e sur les lignes.
Ensuite, on rempli le tableau :
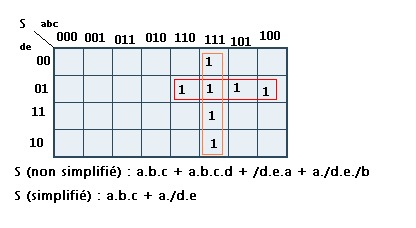
Voici comment procéder morceau par morceau :
- Rappelons déjà l'équation entière : S =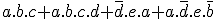
-> Pour a.b.c, j'ai pris la colonne où a, b et c valent 1 et je l'ai entièrement remplie, en effet, comme on ne me donne aucune information sur d et e, on rempli !
-> Pour a.b.c.d, j'ai pris la colonne où a, b, c valent 1 et les lignes où d vaut 1. Rien à remplir comme il y avait déjà des 1 placés à cause du premier morceaux.
 On ne place pas plusieurs 1 dans une case même si les morceaux d'équations "le veulent".
On ne place pas plusieurs 1 dans une case même si les morceaux d'équations "le veulent".
-> Pour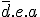 , j'ai pris les colonnes où a vaut 1 et la ligne où d vaut 0 et e 1.
, j'ai pris les colonnes où a vaut 1 et la ligne où d vaut 0 et e 1.
-> Pour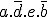 , j'ai pris les lignes où a vaut 1 et b vaut 0, et où d vaut 0 et e vaut 1 ; il n'y a rien besoin de placer, il y avait déjà les 1 !
, j'ai pris les lignes où a vaut 1 et b vaut 0, et où d vaut 0 et e vaut 1 ; il n'y a rien besoin de placer, il y avait déjà les 1 !
Conclusion : l'équation a été beaucoup simplifiée et simplement !
Voila, j'espère que ce tutoriel vous a plu et que vous avez compris malgré mes difficultés pour écrire clairement...
Si vous avez un problème, n'hésitez pas à m'envoyer un message privé, j'y répondrai avec grand plaisir !
(Ben oui, ça fait plaisir de se savoir lu )
)
Mises à jour : 13 octobre 2009 : Ajout de LaTeX pour une meilleure lisibilité. Conversion dans diverses bases
Posté 12 oct. 2008
Dans ce tutoriel, je vais vous apprendre à convertir du :
- Décimal au binaire et à l'hexadécimal.
- Binaire au décimal et à l'hexadécimal.
- Hexadécimal au décimal et au binaire.
C'est très simple une fois la méthode acquise !
Mais n'attendons pas, commençons à attaquer tout de suite !
Sommaire :
1. Du décimal vers le binaire
2. Du décimal vers l'hexadécimal
3. Du binaire au décimal
4. De l'hexadécimal au décimal
5. De l'hexadécimal au binaire
6. Du binaire à l'hexadécimal
7. Grand exercice
Du décimal vers le binaire
Pour convertir du décimal vers le binaire, il faut additionner toutes les puissances de 2 que contient le chiffre en commençant par la plus grande pour retomber à ce chiffre.
Ma phrase étant assez compliquée (j'explique très mal >.<), je vais tout de suite vous montrer un exemple.
Tout d'abord, rappelons quelques puissances de 2 pour nous aider :
2 puissance ... Est égal à ... 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 11 2048 12 4096
Convertissons 563 en binaire :
La puissance de 2 la plus proche que peut contenir 563 est 512.
Ensuite il faut trouver la somme des puissances de deux qui font 563 en commençant par la plus grande (ici 1024 serait inutile comme il est trop grand, on commence donc par 512).
Revenons donc à nos moutons chiffres :
563 = 512*1 + 256*0 + 128*0 + 64*0 + 32*1 + 16*1 + 8*0 + 4*0 + 2*1 + 1*1
Voila ! On sait maintenant que 563 en binaire est 1000110011, car il contient 1 fois 512, 0 fois 256, 0 fois 128, 0 fois 64, 1 fois 32, etc... Facile !
Essayons avec 84 ; la base la plus proche et en dessous de 84 est 64. on commence donc par 64 :
64*1 + 32*0 + 16*1 + 8*0 + 4*1 + 2*0 + 1*0.
84 = 1010100.
Pour vous entrainer, convertissez : 1589, 27, 89, 61 et 985 en binaire, réponses en fin de cour !
Du décimal vers l'hexadécimal
Pour convertir du décimal vers l'hexadécimal, il faut chercher combien de fois il y a la puissance de 16 la plus proche dedans.
Encore une fois, je doute que vous ayez tout compris du premier coup, donc venons en à la pratique.
Voici un petit tableau avec les principales puissances de 16 (tableau très petit vous verrez ).
).
16 puissance ... Est égal à ... 0 1 1 16 2 256 3 4096
Ensuite, il est très important de savoir que que l'hexadécimal va de 0 à 15 mais que à partir de 10, on compte avec les premières lettres de l'alphabet.
Voici l'hexadécimal de 0 à 15 : 0 1 2 3 4 5 6 7 8 9 A B C D E F
Passons maintenant à la pratique, convertissons 563 :
La puissance de 16 la plus proche de 563 et qui est plus petite que 563 est 256 ; on cherche combien de fois il y a 256 dans 563 : 2 fois.
Ensuite on cherche combien de fois il y a 16 (la puissance en dessous de 256) dans le reste de 563-2*256 (=51) : 3 fois.
Enfin, on cherche combien de fois il y a 1 (la puissance en dessous de 16) dans le reste : 3.
Donc, 563 en décimal est égal à 233 en hexadécimal.
Un autre exemple pour mieux comprendre, convertissons 3596 :
3596 = 256*14 + 0*16 + 12 ; donc 3596 = E0C.
Pour vous entrainer, convertissez : 52 653, 2016, 56 et 25 062, corrigé en fin de cour !
Du binaire au décimal
Imaginons que l'on vous donne 111001110 à convertir en décimal, comment faire ? Regardez :
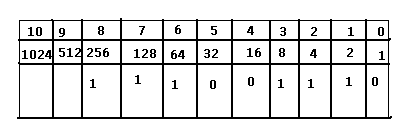
(La première sont les puissances de 2 et la seconde sont les nombres qui leurs correspondent).
Comme vous pouvez le voir, il vous suffit de faire un tableau et d'y placer les chiffres en partant de la droite vers la gauche. Ensuite, il faut additionner là où il y a des 1 dans la tableau, ici cela nous donne : 2 + 4 + 8 + 64 + 128 + 256 = 462.
Nota : Vous pouvez aussi utiliser ce tableau pour convertir du décimal au binaire, en plaçant un 1 dedans dès qu'il y a une puissance de 2 à ajouter ; essayez !
Essayer de traduire : 1001101, 1010101001, 11111, 10100001, corrigé en fin de cours !
De l'hexadécimal au décimal
Alors là, c'est très simple, imaginons que nous voulons traduire 956 en décimal, il faut additionner les puissances de 16 une à une en partant de la droite, ici, 956 = 1*6 + 16*5 + 256*9 = 2390 !
Pour vous entrainer, essayez de convertir : F05, 256, 9B6 et ACE, corrigé en fin de cours !
De l'hexadécimal au binaire
C'est encore une fois, très simple, il faut traduire chiffre après chiffre, en partant de la gauche, du décimal au binaire. Mais, qu'est ce que le décimal vient faire ici me direz vous ? C'est très simple, regardez :
Pour traduire 563 (qui est en hexadécimal), en binaire, il faut traduire 5 en binaire, 6 en binaire et 3 en binaire et placer tout cela un à côté de l'autre !
Donc pour 563 : 5 = 101, 6 = 110 et 3 = 11,
donc 563 en hexadécimal est égal à 10111011 en binaire ! => C'est FAUX, il faut toujours faire des "paquets de 4", c'est à dire que dès qu'un paquet est plus petit, il faut lui rajouter des 0 devant pour qu'il fasse une taille de 4, donc 563 en binaire = 010101100011, et encore ici, la méthode dit qu'il ne faut pas faire un groupement de 4 pour la première particule de la gauche, on doit donc enlever le premier 0, finalement, 563(hexadécimal) = 10101100011 !
Ca parait compliqué mais en réalité c'est simple !
Essayons avec 2E3 : 9 = 10, E = 1110 et 3 = 11, ici, on ne doit pas rajouter de zéro au premier membre, donc il reste 10, le second fait déjà un paquet de 4, donc on ne touche à rien, et le dernier ne fait qu'un paquet de 2, donc on rajoute 2 zéros devant, donc 2E3(hexadécimal) = 1011100011 !
Essayez de traduire : EFB, 256, 532 et 2F !
Réponses en fin de cours !
Du binaire à l'hexadécimal
C'est tout simplement l'inverse que pour de l'hexadécimal au binaire !
On prend des paquets de 4 en commençant par la droite et on converti en décimal !
Par exemple, prenons 101110110, faisons les paquets de 4 : 1(il est tout devant et n'a pas besoin de 0 en plus), 0111 et 0110.
1 = 1, 0111 = 7 et 0110 = 6, donc 101110110 = 176(hexadécimal).
Pour vous entrainer, traduisez : 100110, 1110110 et 1101.
Grand exercice
Pour "finaliser" votre apprentissage, essayez de traduire ceci :
- 674(décimal) à traduire en binaire et en hexadécimal ;
- 1011101010 à traduire en décimal et en hexadécimal ;
- 1F2(hexadécimal) à traduire en décimal et binaire.
Je donne toutes les réponses dans la partie suivante !
CORRECTIONS
1- Exercice du 1) :
1589 = 11101000011 ;
27 = 11011 ;
89 = 1011001;
61 = 111101;
985 = 1111011001.
2- Exercice du 2) :
52 653 = CDAD;
2016 = 7E0;
56 = 38;
25 062 = 61E6;
3- Exercice du 3) :
1001101 = 77;
1010101001 = 681;
11111 = 31;
10100001 = 161;
4- Exercice du 4) :
F05 = 3845;
256 = 598;
9B6 = 2486;
ACE = 2766;
5- Exercice du 5) :
EFB = 111011111011;
256 = 1001010110;
532 = 10100110010;
EF = 11101111;
6- Exercice du 6) :
100110 = 26;
1110110 = 76;
1101 = D;
7- Grand exercice :
674(décimal) = 1010100010 et 2A2.
1011101010 = 746(décimal) et 2EA.
1F2 = 498 et 111110010.
Voila, ici s'achève le tutoriel, certes long, mais très facile à comprendre avec un peu d'entrainement !
Surtout n'hésitez pas à venir faire vos critiques sur le forum pour m'aider à mieux rédiger ! Et si vous ne comprenez pas quelque chose (ou si vous trouvez une faute o_O ), envoyez moi un message privé !
Merci d'avoir lu jusqu'au bout !
Si vous avez du mal avec les simplifications faites "à la main", alors ce tutoriel est fait pour vous car la méthode est assez simple et efficace à 100%.
La table de vérité
Tout d'abord sachez que le plus couramment vous rencontrerez des tables de vérité avec 4 entrées ; les tables avec plus d'entrées sont plus rares, en général.
Je vais donc ici vous exposer une table de vérité avec 4 variables d'entrées et 2 sorties ; je vous montrerez quand même, par la suite, un tableau de Karnaugh avec 5 variables d'entrées.
Soit la table de vérité suivante, avec a, b, c et d comme variables d'entrée et S1 et H1 comme variables de sortie. Comme il y a 4 variables d'entrée, il faut 2^4 (16) lignes, allant du 0 binaire, au 15 binaire ; en sachant que les 0 ou les 1 veulent dire "ouvert" ou "fermé".
 Les "X" sont les impossibilités technologiques, c'est à dire que c'est un état impossible à réaliser dans la réalité ; comme par exemple un capteur qui détecte une pièce trop grande et un capteur qui détecte une pièce trop petite activés en même temps. Ces impossibilités nous seront quand même utiles plus tard.
Les "X" sont les impossibilités technologiques, c'est à dire que c'est un état impossible à réaliser dans la réalité ; comme par exemple un capteur qui détecte une pièce trop grande et un capteur qui détecte une pièce trop petite activés en même temps. Ces impossibilités nous seront quand même utiles plus tard.
Vous pouvez déjà observer que j'ai placé une impossibilité technologique à la 8ième ligne.
Il faut maintenant établir les équations de nos sorties, c'est à dire, écrire la valeur de a, b, c et d quand la sortie vaut 1. Si la sortie vaut 1 et que a vaut 0 par exemple, on notera alors
 .
.S1 =
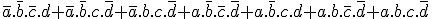
S2 =
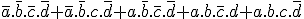
 Rappel : le symbole '.' signifie "et" et le symbole '+' signifie "ou".
Rappel : le symbole '.' signifie "et" et le symbole '+' signifie "ou".Vous pouvez aussi constater que les impossibilités technologiques ne sont pas représentées dans l'équation.
Le tableau de Karnaugh
Voici à quoi doit ressembler le tableau de Karnaugh vide pour S1 dans notre cas :

Nous pouvons constater que :
- Le tableau contient 16 cases, 4 colonnes (variables a et
- Les cases sont "numérotées" en ne faisant changer qu'une seule variable à la fois => 00, 01, 11, 10 ; une seule variable est modifiée à chaque fois.
- Dans les colonnes, 00 signifie
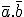 , 01 signifie
, 01 signifie 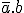 , 11 signifie a.b et 10 signifie
, 11 signifie a.b et 10 signifie 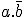 .
.- Dans les lignes, c'est pareil, 00 =>
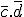 , 01 =>
, 01 => 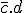 , 11 => c.d et 10 =>
, 11 => c.d et 10 => 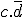 .
.Maintenant, nous pouvons remplir notre tableau ; je vous met l'exemple tout de suite pour mieux comprendre.

Comment l'ais-je rempli ? C'est simple, la première expression est : /a./b./c.d, j'ai donc pris dans le tableau la colonne 00 (/a./
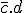 ) et j'y est mis un 1 dedans. Il faut répéter cette action pour tous les morceaux de l'équation.
) et j'y est mis un 1 dedans. Il faut répéter cette action pour tous les morceaux de l'équation.Vous avez aussi pu remarquer que maintenant j'ai placé l'impossibilité technologique (le "X") dans le tableau ; il va nous servir pour la simplification.
Venons en à la simplification :
S1 (non simplifié) =
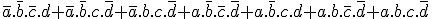 .
.S1 (simplifié) =
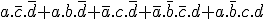 .
.Mais comment ais-je trouvé cela ? C'est très simple, regardez :

La méthode et les règles :
- Cette méthode ne marche que si l'équation ne comporte pas de parenthèses ni de barre sur plusieurs variables ! Si vous avez des parenthèses, développez d'abord pour ne plus en avoir, et si vous avez une barre sur plusieurs éléments, utilisez le théorème de De Morgan.
- Regroupez les "1" par paquets de puissance de 2 (1,2,4,8,16...) ;
- Il faut vous imaginer le tableau comme une sphère, c'est à dire que un "1" étant placé tout en haut à droite pourra se regrouper avec un "1" placé tout en haut à gauche ou bien avec un "1" placé tout en bas à droite ;
- Il est interdit de faire des groupements en diagonale, donc il n'y a que des groupements carrés et rectangles ;
- Pour que l'équation soit simplifiée au maximum, il faut que tous les "1" soient englobés dans le plus grand groupement possible, vous pouvez "utiliser" plusieurs fois le même un si il permet de faire un plus grand groupement avec d'autres 1 (cf. le rose et le orange de S1 par exemple) ;
- Il faut séparer vos groupement d'équation par un "ou" (le symbole "+") ;
- Regardez si les impossibilités technologiques vous permettent de faire un plus grand paquet (dans notre cas il n'y avait qu'une seule impossibilité et elle ne nous permettait pas de faire un paquet plus grand), de plus, il ne faut pas faire de paquet avec les impossibilités technologiques ;
- Ne prenez que l'état des variables qui ne changent pas, par exemple, observons le groupement de couleur orange : comme le tableau est sphérique, le 1 en haut et le 1 en bas sont sensés se toucher, et comme il n'y a pas de 1 permettant de faire un groupement plus grand, le groupement sera de deux ; ensuite, nous pouvons que pour le groupement observé, sur les colonnes, le 1 est placé sur la 3ième colonne où a et b valent 1 et sur la première et dernière ligne où c et d valent respectivement 0 et 0 et 1 et 0. Pour a et b, pas de problème, les deux variables valent 1 tout le temps, le bout d'équation est donc a.b, mais pour c et d, seulement le c change, donc il faut l'ignorer, on ne garde que le d qui vaut toujours 0 ; le bout d'équation complet est donc
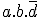 .
.Répétez cette action pour tous les groupements et vous aurez votre équation simplifiée au maximum ! Si vous avez des 1 avec lesquels il est impossible de faire un groupement, alors faite comme si il était dans un groupement, notez l'équation des valeurs des variables qui ne changent pas, pour un 1 seul, aucune variable ne changera donc. (Par exemple, avec le "1 rouge", a et b valent tous les deux 0 et c et d valent 0 et 1, le bout d'équation est donc :
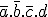 .
.Il est parfois possible de faire des groupements différents mais les résultats seront simplifiés au mêmes degrés.
Maintenant, je vous laisse réfléchir pour H1 ! Je vous met la réponse ci dessous.
Surtout n'hésitez pas à relire, au début ça semble difficile alors que en fait, c'est très simple.
(De plus, je ne suis pas très bon pédagogue :| ).
Solution de H1 :

Autre exemple
Soit l'équation suivante :
S =
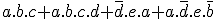 .
.On peut déjà constater qu'il y a cinq variables et non plus quatre !
Voici à quoi ressemble une table de Karnaugh avec cinq entrées :

Vous pouvez constater que j'ai mis a,b et c sur les colonnes et d et e sur les lignes.
Ensuite, on rempli le tableau :

Voici comment procéder morceau par morceau :
- Rappelons déjà l'équation entière : S =
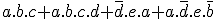
-> Pour a.b.c, j'ai pris la colonne où a, b et c valent 1 et je l'ai entièrement remplie, en effet, comme on ne me donne aucune information sur d et e, on rempli !
-> Pour a.b.c.d, j'ai pris la colonne où a, b, c valent 1 et les lignes où d vaut 1. Rien à remplir comme il y avait déjà des 1 placés à cause du premier morceaux.
 On ne place pas plusieurs 1 dans une case même si les morceaux d'équations "le veulent".
On ne place pas plusieurs 1 dans une case même si les morceaux d'équations "le veulent".-> Pour
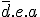 , j'ai pris les colonnes où a vaut 1 et la ligne où d vaut 0 et e 1.
, j'ai pris les colonnes où a vaut 1 et la ligne où d vaut 0 et e 1.-> Pour
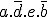 , j'ai pris les lignes où a vaut 1 et b vaut 0, et où d vaut 0 et e vaut 1 ; il n'y a rien besoin de placer, il y avait déjà les 1 !
, j'ai pris les lignes où a vaut 1 et b vaut 0, et où d vaut 0 et e vaut 1 ; il n'y a rien besoin de placer, il y avait déjà les 1 !Conclusion : l'équation a été beaucoup simplifiée et simplement !
Voila, j'espère que ce tutoriel vous a plu et que vous avez compris malgré mes difficultés pour écrire clairement...
Si vous avez un problème, n'hésitez pas à m'envoyer un message privé, j'y répondrai avec grand plaisir !
(Ben oui, ça fait plaisir de se savoir lu
Mises à jour : 13 octobre 2009 : Ajout de LaTeX pour une meilleure lisibilité. Conversion dans diverses bases
Posté 12 oct. 2008
Dans ce tutoriel, je vais vous apprendre à convertir du :
- Décimal au binaire et à l'hexadécimal.
- Binaire au décimal et à l'hexadécimal.
- Hexadécimal au décimal et au binaire.
C'est très simple une fois la méthode acquise !
Mais n'attendons pas, commençons à attaquer tout de suite !
Sommaire :
1. Du décimal vers le binaire
2. Du décimal vers l'hexadécimal
3. Du binaire au décimal
4. De l'hexadécimal au décimal
5. De l'hexadécimal au binaire
6. Du binaire à l'hexadécimal
7. Grand exercice
Du décimal vers le binaire
Pour convertir du décimal vers le binaire, il faut additionner toutes les puissances de 2 que contient le chiffre en commençant par la plus grande pour retomber à ce chiffre.
Ma phrase étant assez compliquée (j'explique très mal >.<), je vais tout de suite vous montrer un exemple.
Tout d'abord, rappelons quelques puissances de 2 pour nous aider :
2 puissance ... Est égal à ... 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 11 2048 12 4096
Convertissons 563 en binaire :
La puissance de 2 la plus proche que peut contenir 563 est 512.
Ensuite il faut trouver la somme des puissances de deux qui font 563 en commençant par la plus grande (ici 1024 serait inutile comme il est trop grand, on commence donc par 512).
Revenons donc à nos moutons chiffres :
563 = 512*1 + 256*0 + 128*0 + 64*0 + 32*1 + 16*1 + 8*0 + 4*0 + 2*1 + 1*1
Voila ! On sait maintenant que 563 en binaire est 1000110011, car il contient 1 fois 512, 0 fois 256, 0 fois 128, 0 fois 64, 1 fois 32, etc... Facile !
Essayons avec 84 ; la base la plus proche et en dessous de 84 est 64. on commence donc par 64 :
64*1 + 32*0 + 16*1 + 8*0 + 4*1 + 2*0 + 1*0.
84 = 1010100.
Pour vous entrainer, convertissez : 1589, 27, 89, 61 et 985 en binaire, réponses en fin de cour !
Du décimal vers l'hexadécimal
Pour convertir du décimal vers l'hexadécimal, il faut chercher combien de fois il y a la puissance de 16 la plus proche dedans.
Encore une fois, je doute que vous ayez tout compris du premier coup, donc venons en à la pratique.
Voici un petit tableau avec les principales puissances de 16 (tableau très petit vous verrez
16 puissance ... Est égal à ... 0 1 1 16 2 256 3 4096
Ensuite, il est très important de savoir que que l'hexadécimal va de 0 à 15 mais que à partir de 10, on compte avec les premières lettres de l'alphabet.
Voici l'hexadécimal de 0 à 15 : 0 1 2 3 4 5 6 7 8 9 A B C D E F
Passons maintenant à la pratique, convertissons 563 :
La puissance de 16 la plus proche de 563 et qui est plus petite que 563 est 256 ; on cherche combien de fois il y a 256 dans 563 : 2 fois.
Ensuite on cherche combien de fois il y a 16 (la puissance en dessous de 256) dans le reste de 563-2*256 (=51) : 3 fois.
Enfin, on cherche combien de fois il y a 1 (la puissance en dessous de 16) dans le reste : 3.
Donc, 563 en décimal est égal à 233 en hexadécimal.
Un autre exemple pour mieux comprendre, convertissons 3596 :
3596 = 256*14 + 0*16 + 12 ; donc 3596 = E0C.
Pour vous entrainer, convertissez : 52 653, 2016, 56 et 25 062, corrigé en fin de cour !
Du binaire au décimal
Imaginons que l'on vous donne 111001110 à convertir en décimal, comment faire ? Regardez :

(La première sont les puissances de 2 et la seconde sont les nombres qui leurs correspondent).
Comme vous pouvez le voir, il vous suffit de faire un tableau et d'y placer les chiffres en partant de la droite vers la gauche. Ensuite, il faut additionner là où il y a des 1 dans la tableau, ici cela nous donne : 2 + 4 + 8 + 64 + 128 + 256 = 462.
Nota : Vous pouvez aussi utiliser ce tableau pour convertir du décimal au binaire, en plaçant un 1 dedans dès qu'il y a une puissance de 2 à ajouter ; essayez !
Essayer de traduire : 1001101, 1010101001, 11111, 10100001, corrigé en fin de cours !
De l'hexadécimal au décimal
Alors là, c'est très simple, imaginons que nous voulons traduire 956 en décimal, il faut additionner les puissances de 16 une à une en partant de la droite, ici, 956 = 1*6 + 16*5 + 256*9 = 2390 !
Pour vous entrainer, essayez de convertir : F05, 256, 9B6 et ACE, corrigé en fin de cours !
De l'hexadécimal au binaire
C'est encore une fois, très simple, il faut traduire chiffre après chiffre, en partant de la gauche, du décimal au binaire. Mais, qu'est ce que le décimal vient faire ici me direz vous ? C'est très simple, regardez :
Pour traduire 563 (qui est en hexadécimal), en binaire, il faut traduire 5 en binaire, 6 en binaire et 3 en binaire et placer tout cela un à côté de l'autre !
Donc pour 563 : 5 = 101, 6 = 110 et 3 = 11,
donc 563 en hexadécimal est égal à 10111011 en binaire ! => C'est FAUX, il faut toujours faire des "paquets de 4", c'est à dire que dès qu'un paquet est plus petit, il faut lui rajouter des 0 devant pour qu'il fasse une taille de 4, donc 563 en binaire = 010101100011, et encore ici, la méthode dit qu'il ne faut pas faire un groupement de 4 pour la première particule de la gauche, on doit donc enlever le premier 0, finalement, 563(hexadécimal) = 10101100011 !
Ca parait compliqué mais en réalité c'est simple !
Essayons avec 2E3 : 9 = 10, E = 1110 et 3 = 11, ici, on ne doit pas rajouter de zéro au premier membre, donc il reste 10, le second fait déjà un paquet de 4, donc on ne touche à rien, et le dernier ne fait qu'un paquet de 2, donc on rajoute 2 zéros devant, donc 2E3(hexadécimal) = 1011100011 !
Essayez de traduire : EFB, 256, 532 et 2F !
Réponses en fin de cours !
Du binaire à l'hexadécimal
C'est tout simplement l'inverse que pour de l'hexadécimal au binaire !
On prend des paquets de 4 en commençant par la droite et on converti en décimal !
Par exemple, prenons 101110110, faisons les paquets de 4 : 1(il est tout devant et n'a pas besoin de 0 en plus), 0111 et 0110.
1 = 1, 0111 = 7 et 0110 = 6, donc 101110110 = 176(hexadécimal).
Pour vous entrainer, traduisez : 100110, 1110110 et 1101.
Grand exercice
Pour "finaliser" votre apprentissage, essayez de traduire ceci :
- 674(décimal) à traduire en binaire et en hexadécimal ;
- 1011101010 à traduire en décimal et en hexadécimal ;
- 1F2(hexadécimal) à traduire en décimal et binaire.
Je donne toutes les réponses dans la partie suivante !
CORRECTIONS
1- Exercice du 1) :
1589 = 11101000011 ;
27 = 11011 ;
89 = 1011001;
61 = 111101;
985 = 1111011001.
2- Exercice du 2) :
52 653 = CDAD;
2016 = 7E0;
56 = 38;
25 062 = 61E6;
3- Exercice du 3) :
1001101 = 77;
1010101001 = 681;
11111 = 31;
10100001 = 161;
4- Exercice du 4) :
F05 = 3845;
256 = 598;
9B6 = 2486;
ACE = 2766;
5- Exercice du 5) :
EFB = 111011111011;
256 = 1001010110;
532 = 10100110010;
EF = 11101111;
6- Exercice du 6) :
100110 = 26;
1110110 = 76;
1101 = D;
7- Grand exercice :
674(décimal) = 1010100010 et 2A2.
1011101010 = 746(décimal) et 2EA.
1F2 = 498 et 111110010.
Voila, ici s'achève le tutoriel, certes long, mais très facile à comprendre avec un peu d'entrainement !
Surtout n'hésitez pas à venir faire vos critiques sur le forum pour m'aider à mieux rédiger ! Et si vous ne comprenez pas quelque chose (ou si vous trouvez une faute o_O ), envoyez moi un message privé !
Merci d'avoir lu jusqu'au bout !














