Hi All,
I am truly inspired by Oracid's development of quadrupeds. I am going to attempt to repeat his work using my own style. I would think of this as a 'peer review' process. Perhaps in trying to repeat the progress we all learn something new and innovative.
I think a lot of my design principles are similar to others in the forum. Simple solutions, using commonly available (affordable) parts. I like to use 3D printed parts. I design all my parts using OpenSCAD.
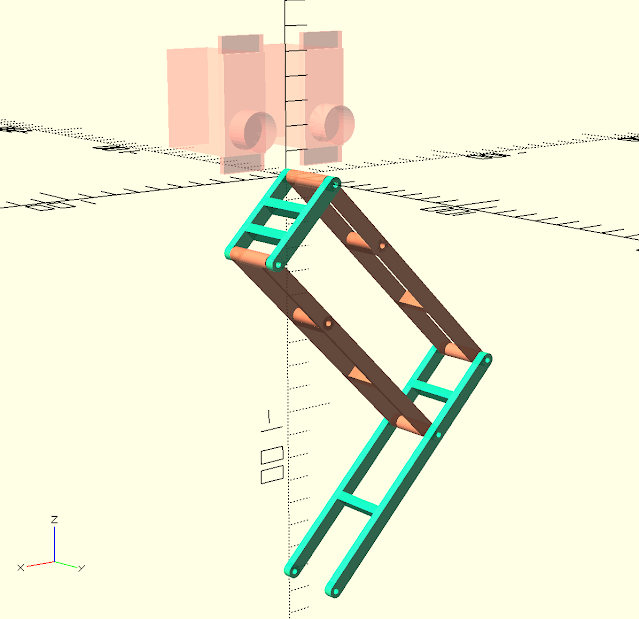
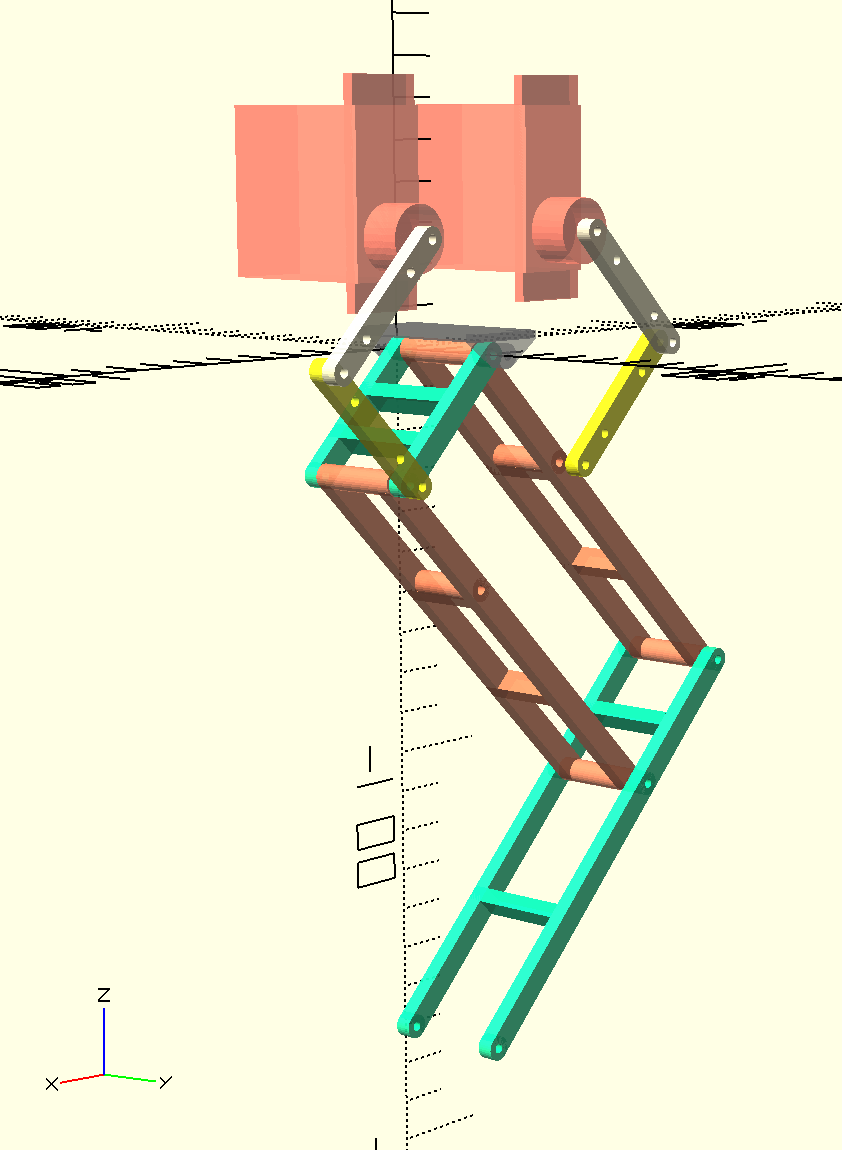
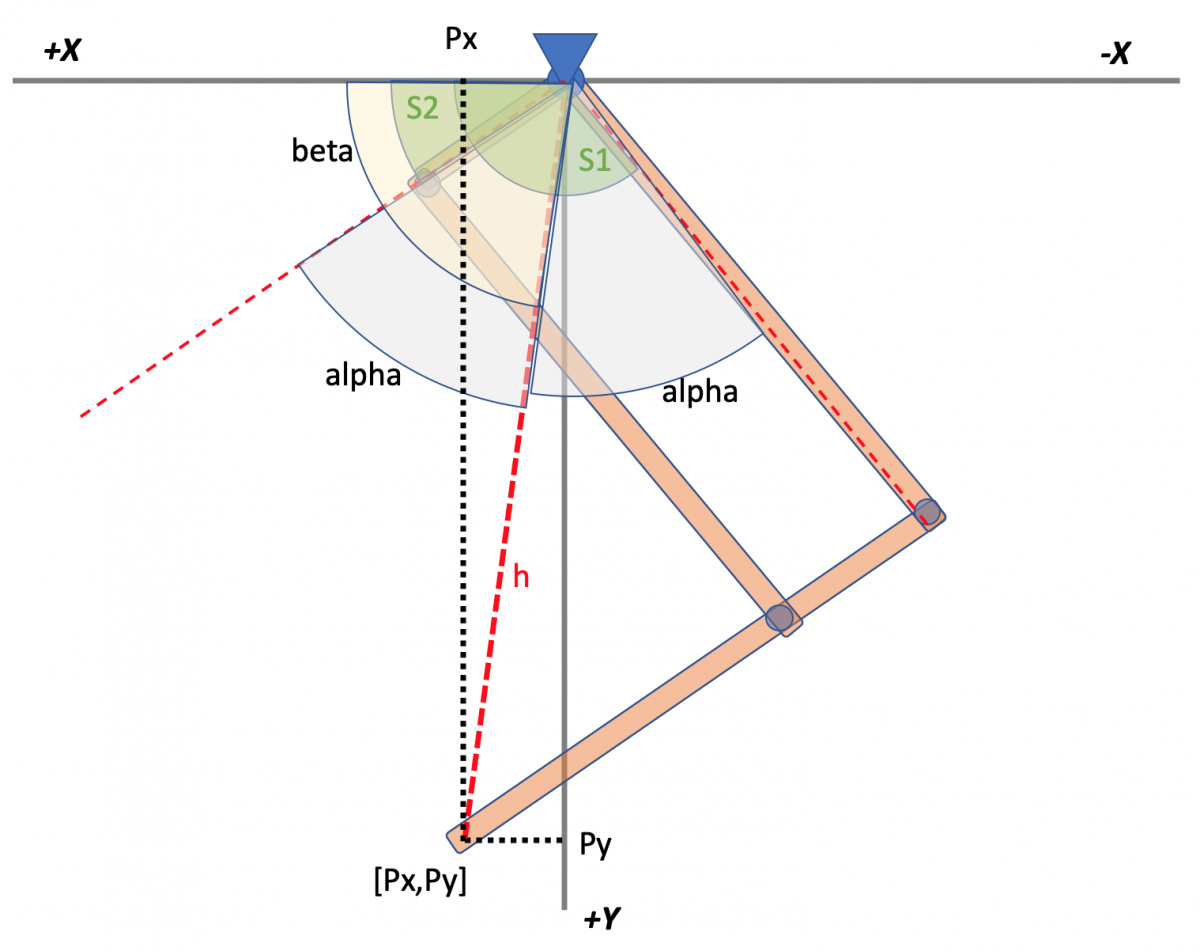
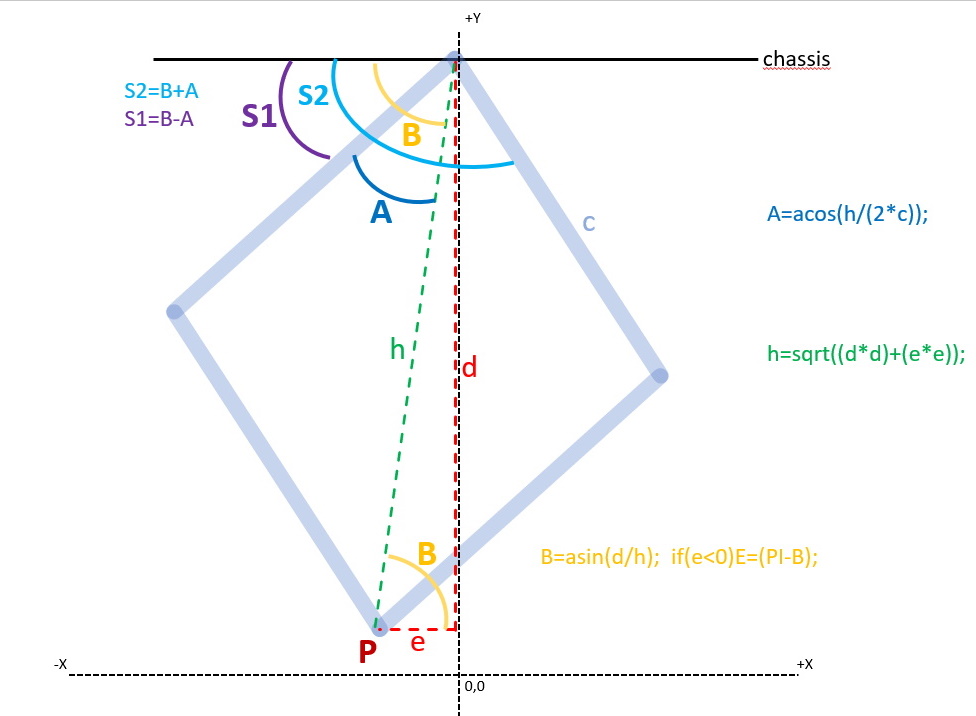
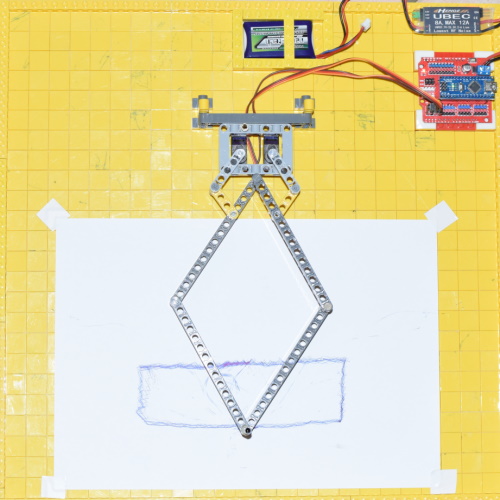
Mojo4 will be my 4th quadruped design. I have tried different styles of legs. the 5 bar looks to be very promising. I really like that the leg joint is supported directly at the chassis, and not completely at the servo.
For this leg I am going attempt using a 'hinge' type joint. The hinge will be 3D print and the pin will be a small nail (clou). I believe this will be enough for the actuation, and provide rigid stability against wobble. We shall see.
Right now I am focused on the basics of getting the leg to work with the 5Bar technique:
Questions for the experts ... ![]()
1) did you find any suggested/magic ratio for the separation between the 2 servos?
2) did you find any suggested/magic length ratio for the 'control arms' the lifters (l1) and (p1) ?? I am reading old posts to see what you all discussed. any helpful suggestions!
-- right now I am planning on L & P to be identical in length and form a 90 degree angle with the 5Bar ©
Thanks,
(TNERA) - Doug